Chapter 1 Introduction to R

Figure 1.1: A Young Statypus Makes his First Mark on the World
The platypus is anatomically so unique that when the first specimen was brought to Europe in the 1790s, a curator of London’s Natural History Museum, George Shaw, thought that it was an elaborate hoax and attempted, unsuccessfully, to prove it was just a hoax.7
The R Statistical Programming Language plays a central role in this book. While there are several other programming languages and software packages that do similar things, we chose R for several reasons:
- R is widely used among statisticians, especially academic statisticians. If there is a new statistical procedure developed somewhere in academia, chances are that the code for it will be made available in R. This distinguishes R from, say, Python.
- R is commonly used for statistical analyses in many disciplines. Other software, such as SPSS or SAS are also used and in some disciplines would be the primary choice for some discipline specific courses, but R is popular and its user base is growing.
- R is free. You can install it and all optional packages on your computer at no cost. This is a big difference between R and SAS, SPSS, MATLAB, and most other statistical software.
- R has been experiencing a renaissance. With the advent of the tidyverse and RStudio, R is a vibrant and growing community. We also have found the community to be extremely welcoming. The R ecosystem is one of its strengths.
In this chapter, we will begin to see some of the capabilities of R. We point out that R is a fully functional programming language, as well as being a statistical software package. We will only touch on the nuances of R as a programming language in this book.
1.1 Introduction to RStudio
While R will be the software the actually does most of the calculations we want to do, we will primarily interact with the program called RStudio. RStudio is an open-source integrated development environment (IDE) that enhances the R programming language. It can be used to used to make simple calculations as we will see in Section 1.2, run chunks of code to do more sophisticated statistical calculations as we will see in nearly all chapters of this book, and it can even integrate with the Python coding language to do advanced techniques such as machine learning.
RStudio is an improvement over the base R interface as it allows the user to view four different panels at one time. Users will primarily interact with RStudio in R “scripts” which appear in the upper left panel of the screen. Code the user wishes to run is then sent to the console which appears in the lower left panel of the screen. The upper right panel is typically used to view data and functions that the user has in their own personal environment at the moment, but can also be used to view a history of all lines of code that the software has run. The lower right panel is used for viewing plots, viewing and installing packages, as well as reading help files.
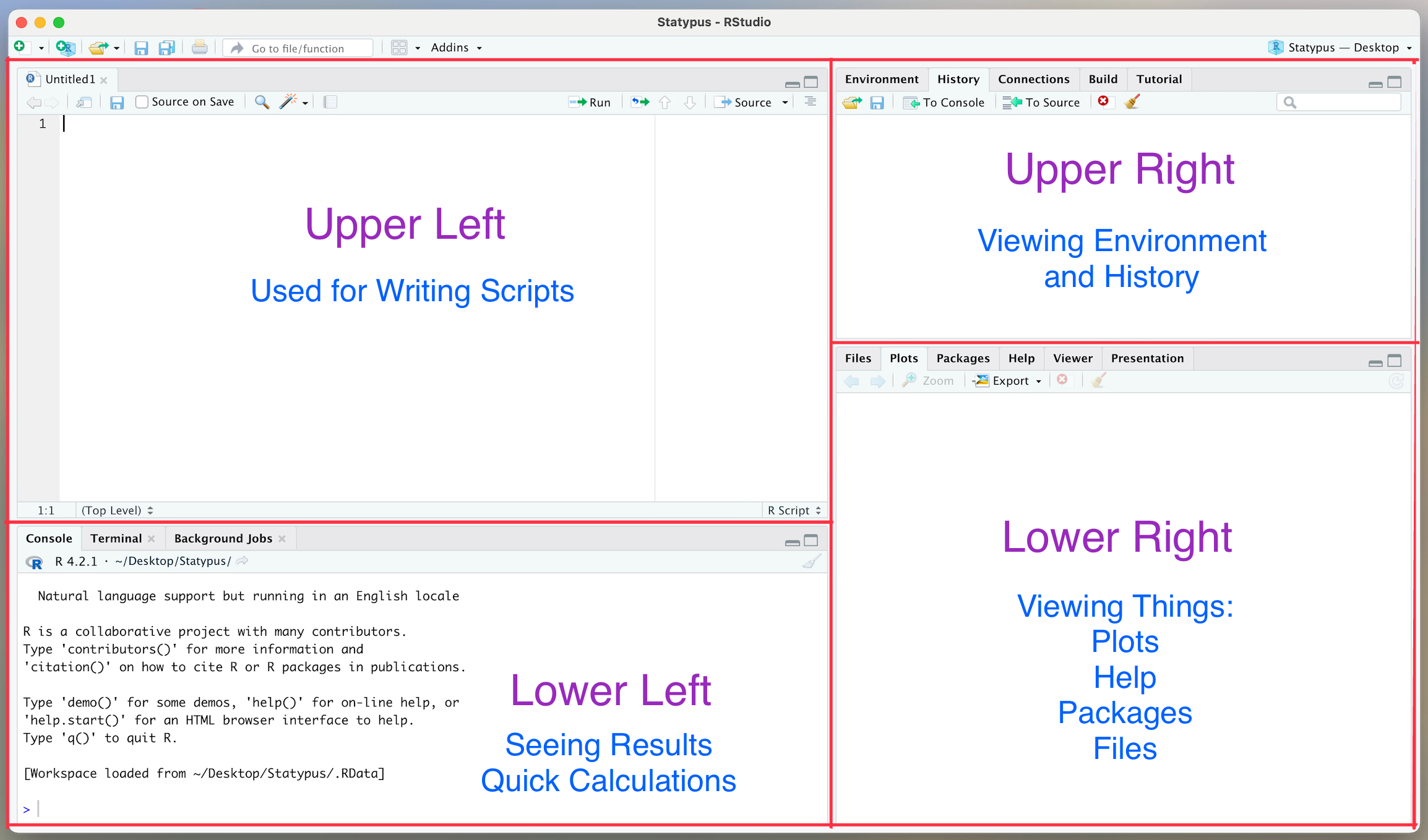
Figure 1.2: The 4 Panels of RStudio
The RStudio environment can be customized and manipulated. The above discussion is based on the default position and uses of the four panels present in the program.
The following video is a quick visual introduction to working within RStudio made by someone not affiliated with Statypus. It goes into more detail than is likely necessary, but is a very solid RStudio introduction video.
1.2 Arithmetic and Variable Assignment
We begin by showing how R can be used as a calculator. Here is a table of commonly used arithmetic operators.
| Operator | Description | Example |
|---|---|---|
+ |
addition | 1 + 1 |
- |
subtraction | 4 - 3 |
* |
multiplication | 3 * 7 |
/ |
division | 8 / 3 |
^ |
exponentiation | 2^3 |
Throughout the book, lines that start with ## indicate output from R commands. These will not show up when you type in the commands yourself. The [1] in Example 1.1 below (and likely all R output in the book) indicate that there is one piece of output from the command. These will show up when you type in the commands.
Example 1.1 The output of the examples in Table 1.1 is given below.
1+1## [1] 24-3## [1] 13*7## [1] 218/3## [1] 2.6666672^3## [1] 8Another useful function is sqrt() which calculates the square root of a number. We will need this when we go to calculate a standard deviation in Chatper 4.
sqrt(9)R also has built in useful constants such as pi which is \(\pi \approx 3.141593\). Here is an example of how you can use pi.8
pi^2/6## [1] 1.644934R is a functional programming language. If you don’t know what that means, that’s OK, but as you might guess from the name, functions play a large role in R. We will see many, many functions throughout the book. Every time you see a new function, think about the following four questions:
- What type of input does the function accept?
- What does the function do?
- What does the function return as output?
- What are some typical examples of how to use the function?
You can’t get very far without storing results of your computations to variables! The way9 to do so is with the arrow <-. Typing Alt + - on a PC or option + - on a Mac are the keyboard shortcuts for <-, but you can also just use the < and - keys on your keyboard.
It is note that this is a directional operation. The line of code below would set the variable x to be the value 2 and it would then appear in the Upper Right panel of RStudio in your Environment.
x <- 2However, running the following line of code will cause an error (we will look at errors and warnings more in Section 1.9).
2 <- x## Error in 2 <- x: invalid (do_set) left-hand side to assignmentHere RStudio is telling us that we have tried to assign the value of x into the constant 2. This is nonsensical and R tells us just that.
This does allow us to write some lines of code that would be paradoxical if we used an equal sign. For example consider the following line of code.
x <- x + 1This line of code takes the existing value of x, adds 1 to it, and then stores it back into the variable x. This is another example of code that would not work if we switched the x and x+1.10
Example 1.2 Consider the following block of code which will convert 30 degrees Celsius to its equivalent in Farhrenheit.
# Value is in degrees Celsius
temperature <- 30
temperature <- temperature*1.8
temperature <- temperature + 32 The # Value is in degrees Celsius part of the code above is a comment. These are provided to give the reader information about what is going on in the R code, but are not executed and have no impact on the output.
Note that none of the above lines actually resulted in the value of temperature being displayed in the console.
If you want to see what value is stored in a variable, you can
1. type the variable name
temperature## [1] 862. look in the environment box in the upper right-hand corner of RStudio as shown below.
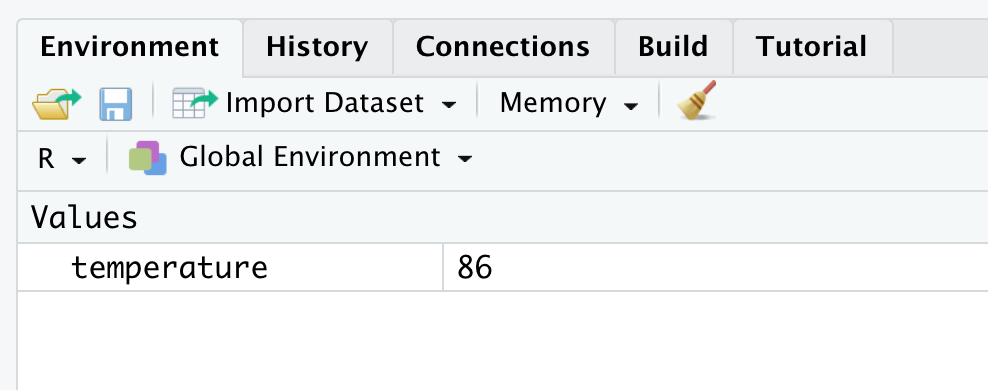
Figure 1.3: Looking at a Value in the Environment
3. Use the str command. This command gives other useful information about the variable, in addition to its value.
str( temperature )## num 86This says that height contains num-eric data, and its current value is 86 (which is \(30*1.8 + 32\)). Note that there is a big difference between typing temperature + 32 (which computes the value of temperature + 32 and displays it on the screen) and typing temperature <- temperature + 32, which computes the value of temperature + 2 and stores the new value back in temperature.
It is important to choose your variable names wisely. Variables in R cannot start with a number, and for our purposes, they should not start with a period.
Do not use T or F as a variable name. Think twice before using c, q, t, C, D, or I as variable names, as they are already defined.
It may also be a bad idea (and is one of the most frustrating things to debug on the rare occasions that it causes problems) to use sum, mean, or other commonly used functions as variable names. T and F are variables with default values TRUE and FALSE, which can be changed.
We recommend writing out TRUE and FALSE rather than using the shortcuts T and F for this reason.**
We also misspoke when we said pi is a constant. It is actually a variable which is set to 3.141593 when R is started, but can be changed to any value you like.11
If you find that a dataset or value such as pi is not acting as you expect and you want to have them return to the default state, you have a couple of choices. You can restart R by clicking on Session in the top row menu and then selecting Restart as shown bloew.
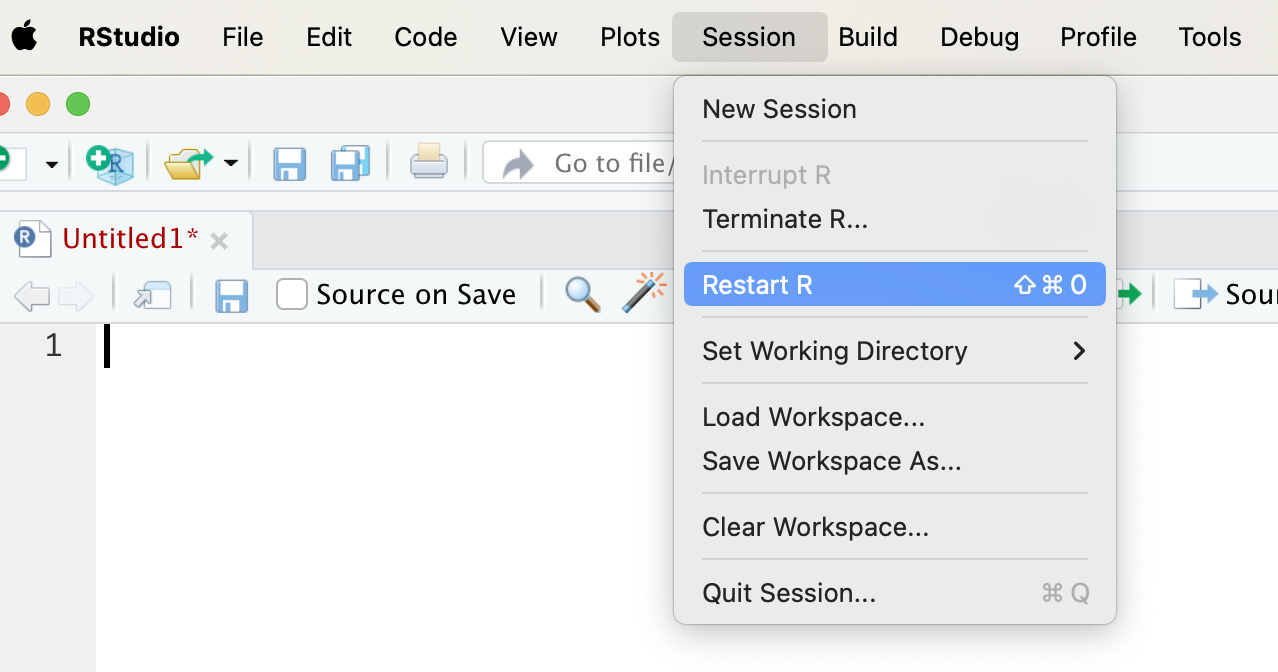
Figure 1.4: How To Restart RStudio Session
This will do more than just reset variables to their default values; it will reset R to its start-up state. If you think you may have messed something up, this is a quick way to “start again.”
You can also remove an object from the R environment by using the function remove function, rm(). The function rm accepts the name of an object and removes it from memory. As an example, look at the code below:
pi## [1] 3.141593pi <- 3.2
pi## [1] 3.2rm( pi )
pi## [1] 3.141593We end this section with a couple more hints. To remove all of the variables from your working environment, click on the broom icon in the Environment tab in RStudio. You may want to do this from time to time, as R can slow down when it has too many large variables in the current environment.
If you begin typing (at least the first three characters of) something into RStudio, auto-complete will search for all things in memory, data or functions, in a non-case-sensitive way and allow you to choose from a drop down list. For example, typing vie into an R script or into the R console it will pop up a menu to allow you to choose the function, View(), as shown below.
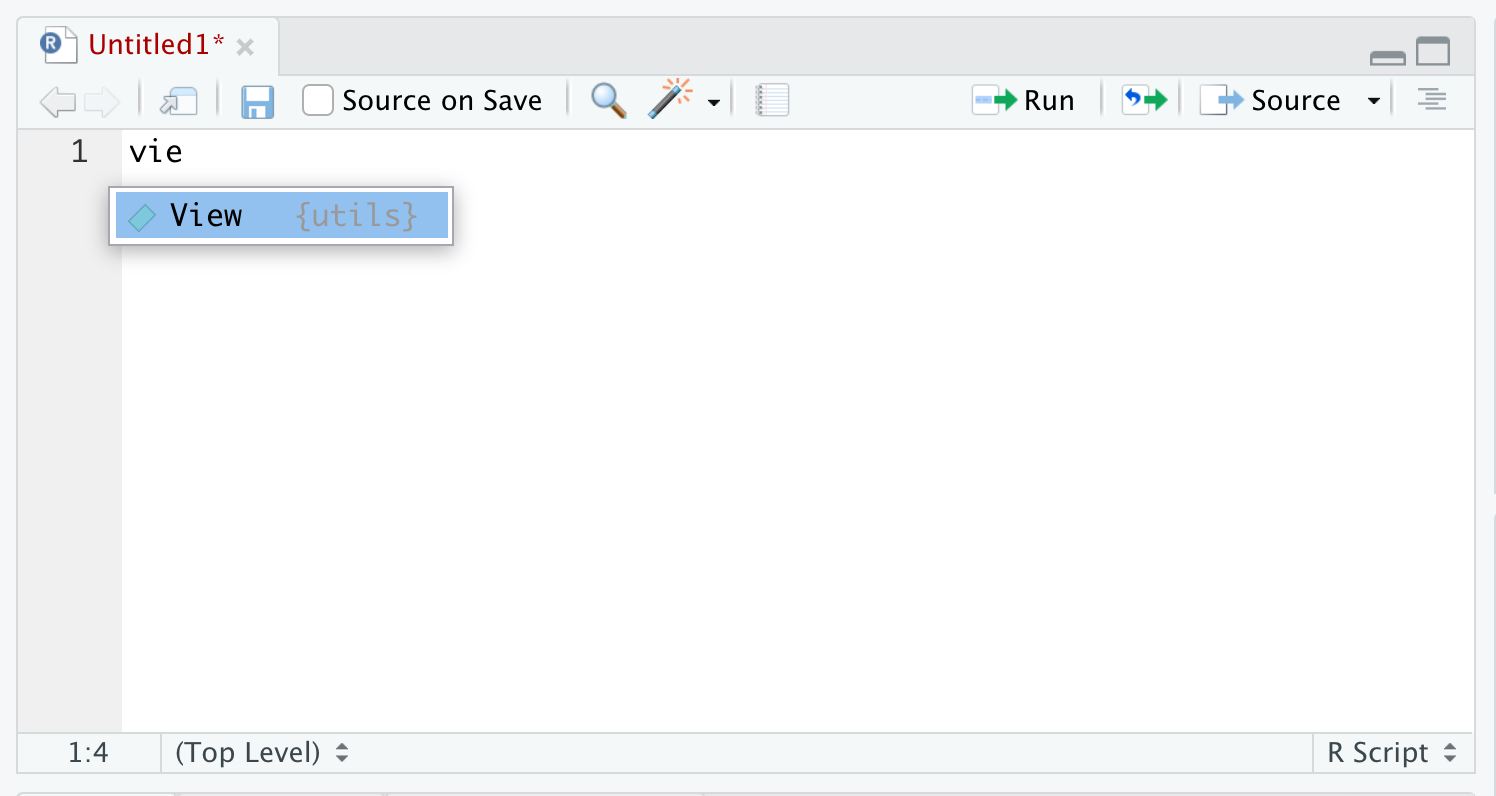
Figure 1.5: Autocomplete Example
If there are more than one option for the three characters for what you type, you get a dropdown showing all of the objects that begin with that regardless of case. For example, below is what you will likely see if you type in bas into R.
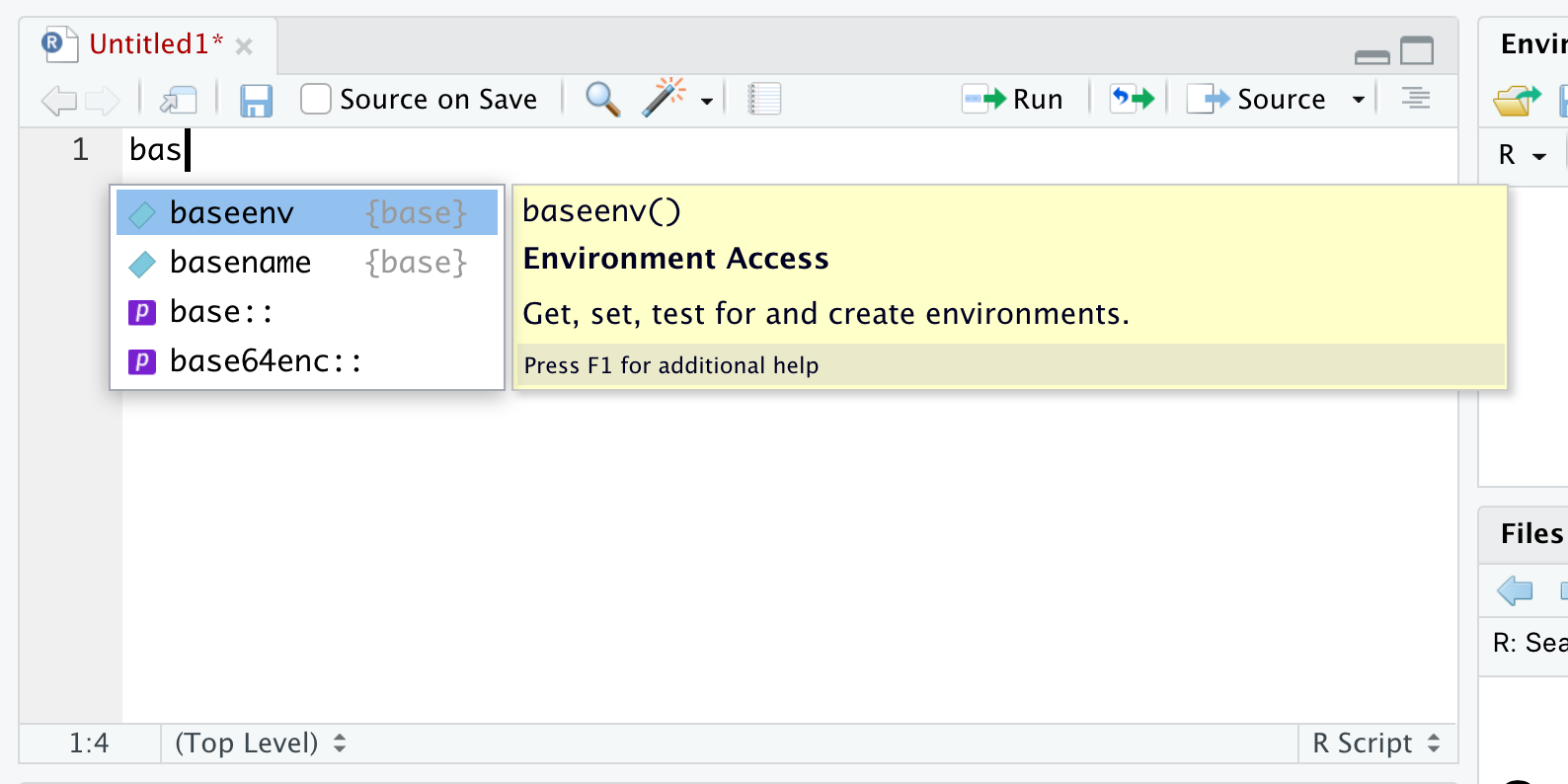
Figure 1.6: Autocomplete Example
At Statypus, we call this the Rule of Type Three: that is, you should type the first three characters of the element you are looking for and then using the menu to select the appropriate value.
Many typos can be avoided by following the Rule of Type Three as R is case-sensitive so that view( rivers ) causes an error while View( rivers ) will display the vector rivers in the upper left panel of RStudio.
view( rivers )## Error in view(rivers): could not find function "view"1.3 Help
R comes with built-in help. In RStudio, there is a help tab in the lower right panel. Placing a ? before an object gives help for that object.
Example 1.3 You can try by typing ?sqrt in the console to see the help page for sqrt.
Help pages in R have some standard headings. Let’s look at some of the main areas in the help page for sqrt. The top portion of the help file is shown below.

Figure 1.7: Help File for the Square Root Function
Description: The help page says that sqrt computes the (principal) square root of x.
Usage: sqrt( x ) means that sqrt takes one arguments, x.
Arguments: x is a numeric or complex vector or array. This might be confusing for now, but the help page indicates that sqrt is more flexible than what we have seen so far.
Examples: The help page provides code that you can copy and paste into the R console to see what the function does. In this case, it provides the code to plot the function \(f(x) = \sqrt{|x|}\) for \(x\) between -9 and 9.
It is important to note that the help file in Example 1.3 contains information about sqrt() as well as the absolute value function, abs(). R sometimes combines the help files for objects that are similar, such as sqrt() and abs().
It can take some time to get used to reading R Documentation. For now, we recommend reading the four headings discussed in Example 1.3 to see whether there are things you can learn about new functions. Don’t worry if there are things in the documentation that you don’t yet understand.
1.4 Vectors
Data often takes the form of multiple values of the same type. In R, multiple values are stored in a data type called a vector. R is designed to work with vectors quickly and easily.
1.4.1 Creating Vectors
There are many ways to create vectors. Perhaps the easiest is the c function:
c( 2, 3, 5, 7, 11 )## [1] 2 3 5 7 11Example 1.4 The c function combines the values given to it into a vector. In this case, the vector is the list of the first 5 prime numbers. We can store vectors in variables just like we did with numbers:
primes <- c( 2, 3, 5, 7, 11 )You can also create a vector of numbers in order using the : operator:
1:10## [1] 1 2 3 4 5 6 7 8 9 10Once you have created a vector, you may also want to do arithmetic or other operations on it. Most of the operations in R work “as expected” with vectors. Suppose you wanted to see what the square roots of the first 5 primes were. You might guess:
sqrt( primes )## [1] 1.414214 1.732051 2.236068 2.645751 3.316625and you would be right! Returning to the cryptic manual entry in sqrt, we recall that it stated that x is a numeric vector. This is the documentation’s way of telling us that sqrt is vectorized. If we supply the square root function with a vector of values, then sqrt will compute the (principal) square root of each value separately. Other commands reduce a vector to a number, for example sum adds all elements of the vector, and max finds the largest.
sum( primes )## [1] 28max( primes )## [1] 11Example 1.5 Another useful function for creating vectors is seq. This is a generalization of the : operator described above. We will not go over the entire list of arguments associated with seq, but we note that it has arguments from, to, by and length.out. We provide a couple of examples that we hope illustrate well enough how to use seq.
seq( from = 1 , to = 11 , by = 2 )## [1] 1 3 5 7 9 11seq( from = 1 , to = 11 , length.out = 21 )## [1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0
## [16] 8.5 9.0 9.5 10.0 10.5 11.0The expression [16] on the second line of the last output of Example 1.5 tells us that 8.5 is the 16th value (out of the 21 determined by length.out) of the vector.
Guess what would happen if you type primes + primes, primes * primes and sum(1/primes) if primes is defined as in Example 1.4. Were you right?
1.4.2 Indexing Vectors
To examine or use a single element in a vector, you need to supply its index. If we have a vector named x, then x[ 1 ] is the first element, x[ 2 ] is the second, and so on.
Example 1.6 Using the primes vector we created in Example 1.4, we can find the first and fourth values with the following two lines of code (and output).
primes[ 1 ]## [1] 2primes[ 4 ]## [1] 7You can do many things with indexes. For example, you can provide a vector of indices, and R will return a new vector with the values associated with those indices.
primes[ 1:3 ]## [1] 2 3 5You can remove a value from a vector by using a - sign.
primes[ -1 ]## [1] 3 5 7 11You can provide a vector of TRUE and FALSE values as an index, and R will return the values that are associated with TRUE.
As a beginner, take care to have the length of the vector of TRUE and FALSE values be the same length as the original vector.
primes[ c( TRUE, FALSE, TRUE, FALSE, TRUE ) ]## [1] 2 5 11The construct of providing a Boolean vector (that is, a vector containing TRUE and FALSE) for indexing is most useful for selecting elements that satisfy some condition. Suppose we wanted to “pull out” the values in primes that are bigger than 6. We create an appropriate vector of TRUE and FALSE values, then index primes by it.
primes > 6## [1] FALSE FALSE FALSE TRUE TRUEprimes[ primes > 6 ]## [1] 7 11Observe the use of > for comparison in Example 1.6. In R (and most modern programming languages), there are some fundamental comparison operators:
==equal to!=not equal to>greater than<less than>=greater than or equal to<=less than or equal to
Another important operator is the %in%, which is TRUE if a value is in a vector. For example:
4 %in% primes## [1] FALSEodds <- seq( from = 1 , to = 11 , by = 2 )
primes[ primes %in% odds ]## [1] 3 5 7 11Example 1.7 R comes with many built-in data sets. For example, the rivers data set is a vector containing the length of major North American rivers. Try typing ?rivers to see some more information about the data set. Let’s see what the data set contains.
rivers## [1] 735 320 325 392 524 450 1459 135 465 600 330 336 280 315 870
## [16] 906 202 329 290 1000 600 505 1450 840 1243 890 350 407 286 280
## [31] 525 720 390 250 327 230 265 850 210 630 260 230 360 730 600
## [46] 306 390 420 291 710 340 217 281 352 259 250 470 680 570 350
## [61] 300 560 900 625 332 2348 1171 3710 2315 2533 780 280 410 460 260
## [76] 255 431 350 760 618 338 981 1306 500 696 605 250 411 1054 735
## [91] 233 435 490 310 460 383 375 1270 545 445 1885 380 300 380 377
## [106] 425 276 210 800 420 350 360 538 1100 1205 314 237 610 360 540
## [121] 1038 424 310 300 444 301 268 620 215 652 900 525 246 360 529
## [136] 500 720 270 430 671 1770By typing ?rivers, we learn that this data set gives the lengths (in miles) of 141 major rivers in North America, as compiled by the US Geological Survey. This data set is explored further in the exercises in this chapter. We will often want to examine only the first few elements when the data set is large. For that, we can use the function head, which by shows the first six elements.
head( rivers )## [1] 735 320 325 392 524 450Example 1.8 The discoveries data set is a vector containing the number of “great” inventions and scientific discoveries in each year from 1860 to 1959. Try ?discoveries to see more information about the discoveries data set. You might try the examples listed there just to see what they do, but we won’t be doing anything like that yet. Let’s see what the data set contains.
discoveries## Time Series:
## Start = 1860
## End = 1959
## Frequency = 1
## [1] 5 3 0 2 0 3 2 3 6 1 2 1 2 1 3 3 3 5 2 4 4 0 2 3 7
## [26] 12 3 10 9 2 3 7 7 2 3 3 6 2 4 3 5 2 2 4 0 4 2 5 2 3
## [51] 3 6 5 8 3 6 6 0 5 2 2 2 6 3 4 4 2 2 4 7 5 3 3 0 2
## [76] 2 2 1 3 4 2 2 1 1 1 2 1 4 4 3 2 1 4 1 1 1 0 0 2 0If we type str( discoveries ) we see that the data set is stored as a time series rather than as a vector. We will return to this data type in Section 5.2. For our purposes in this section, that will be an unimportant distinction, and we can simply think of the variable as a vector of numeric values.
The first ten elements are:
head( discoveries , n = 10 )## [1] 5 3 0 2 0 3 2 3 6 1Here are a few more things you can do with a vector:
sort( discoveries )## [1] 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2
## [26] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3
## [51] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4
## [76] 4 4 4 4 5 5 5 5 5 5 5 6 6 6 6 6 6 7 7 7 7 8 9 10 12sort( discoveries, decreasing = TRUE )## [1] 12 10 9 8 7 7 7 7 6 6 6 6 6 6 5 5 5 5 5 5 5 4 4 4 4
## [26] 4 4 4 4 4 4 4 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
## [51] 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [76] 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0table( discoveries )## discoveries
## 0 1 2 3 4 5 6 7 8 9 10 12
## 9 12 26 20 12 7 6 4 1 1 1 1max( discoveries )## [1] 12sum( discoveries )## [1] 310discoveries[ discoveries > 5 ]## [1] 6 7 12 10 9 7 7 6 6 8 6 6 6 7which( discoveries > 5 ) + 1859## [1] 1868 1884 1885 1887 1888 1891 1892 1896 1911 1913 1915 1916 1922 1929We will use sort() in Chapter 2, but encourage the curious reader to look at the help file by running ?sort in your console. When table is provided a vector, it returns a table of the number of occurrences of each value in the vector. It will not provide zeros for values that are not there, even if it seems “obvious” to a human that there might have been place for that value. We will go over table more fully in Section 3.1.1.
The function which accepts a vector of TRUE and FALSE values, and returns the indices in the vector that are TRUE. So, in the last line of the code in the example above, adding 1859 to the indices gives the years that had more than 5 great discoveries.
In Example 1.8 we ran the following line of code: sort( discoveries, decreasing = TRUE ). This is an example of running an R function and shows the basic syntax we will use, which is shown below.
function( argument1, argument2 )In R, functions can have more than input, we show 2 above, but it can be more. Functions can also have more than one output. This may go against the definition of a function that you learned, but the most important concept is still true. The output of a function is uniquely determined by the arguments that we pass to the function.12
We can see what arguments a function wants by typing in the function, such as sort(), into an R script (or in the Console) and waiting. A yellow pop-up will appear showing the arguments that the function needs passed to it.
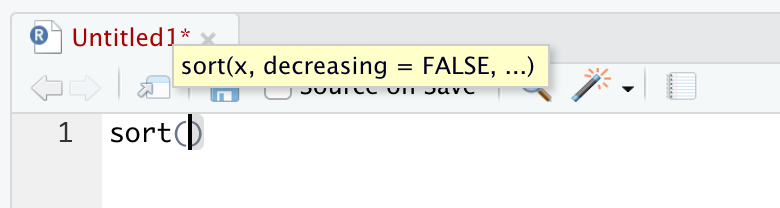
Figure 1.8: The pop-up showing the arguments of sort()
This shows that the main arguments are x, the data to be sorted, and decreasing which is set to FALSE by default as indicated in the pop-up. The ellipsis indicates that there are other, and lesser used, arguments which we can look at by using the help option by running ?sort.
1.5 Data Types
All data in R has a type. Basic types hold one simple object. Data structures are built on top of the basic types. You can always learn the type of your data with the str structure command.
1.5.1 Basic Data Types
There are six basic types in R, although we won’t use complex or raw. Also, it will not be necessary to make a distinction between numeric and integer data in this book, since R converts between types automatically.
numeric: Real numbers, stored as some number of decimal places and an exponent. If you type
x <- 2, thenxwill be stored asnumericdata.integer: Integers. If you type
x <- 2L, thenxwill be stored as an integer.13 When reading data in from files, R will detect if all elements of a vector are integers and store that data as integer type.character: A collection of characters, also called a string. If you type
x <- "hello", thenxis acharactervariable. Comparestr( "hello" )tostr( c( 1, 2 ) ). Note that if you want to access theefromhello, you cannot usex[ 2 ].logical: Either
TRUEorFALSE. The operators!,&, and|perform Boolean logic NOT, AND, and OR, respectively, on logical data.
1.5.2 Other Data Types
There are many different data structures. The most important is the vector, which we have already met. Data Frames are also central to our study and will be described in Section 1.6.
Another important structured type is called a factor:
- factor: Factor data takes on values in a predefined set. The possible values are called the levels. Levels are stored efficiently as numbers, and their names are only used for output. For example, a
ratingvariable might take values high, medium, and low. A variablecontinentcould be set up to allow only entries of Africa, Antarctica, Asia, Australia, Europe, North America, or South America which would then be stored as numbers such as the integers from 1 to 7. Factor type data is common in statistics, and many R functions only work properly when data is in factor form.
Our experience has been that students underestimate the importance of knowing what type of data they are working with. As a first example of the importance of data types, let’s return to the table function. If we use table on a vector of integers, then R simply gives a list of the values that occur together with the number of times that they occur. However, if we use table on a factor, then R gives a list of all possible levels of the factor together with the number of times that they occur, including zeros. See Exercise 1.11 for an example.
R works really well when the data types are assigned properly. However, some bizarre things can occur when you try to force R to do something with a data type that is different than what you think it is!
Whenever you examine a new data set (especially one that you read in from a file and there is no help option), we encourage you to run str() on it, followed by head(). Make sure that the data is stored the way you want before you continue with anything else.
1.5.3 Missing Data
Missing data is a problem that comes up frequently, and R uses the special value NA to represent it. NA isn’t a data type, but a value that can take on any data type. It stands for Not Available, and it means that there is no data collected for that value.
Example 1.9 Consider the vector airquality$Ozone, which is part of base R:
airquality$Ozone## [1] 41 36 12 18 NA 28 23 19 8 NA 7 16 11 14 18 14 34 6
## [19] 30 11 1 11 4 32 NA NA NA 23 45 115 37 NA NA NA NA NA
## [37] NA 29 NA 71 39 NA NA 23 NA NA 21 37 20 12 13 NA NA NA
## [55] NA NA NA NA NA NA NA 135 49 32 NA 64 40 77 97 97 85 NA
## [73] 10 27 NA 7 48 35 61 79 63 16 NA NA 80 108 20 52 82 50
## [91] 64 59 39 9 16 78 35 66 122 89 110 NA NA 44 28 65 NA 22
## [109] 59 23 31 44 21 9 NA 45 168 73 NA 76 118 84 85 96 78 73
## [127] 91 47 32 20 23 21 24 44 21 28 9 13 46 18 13 24 16 13
## [145] 23 36 7 14 30 NA 14 18 20This shows the daily ozone levels (ppb) in New York during the summer of 1973.
We would like to find the average ozone level for that summer, using the R function mean.
However, just applying mean to the data produces an NA:
mean( airquality$Ozone )## [1] NAThis is because the Ozone vector itself contains numerous NA values, corresponding to days when the ozone level was not recorded. Most R functions will force you to decide what to do with missing values, rather than make assumptions. To find the mean ozone level for the days with data, we must specify that the NA values should be removed with the argument na.rm = TRUE:
mean( airquality$Ozone , na.rm = TRUE )## [1] 42.12931We will go over this again in Section 4.1.1 as well as other places where na.rm is helpful.
1.6 Data Frames
Returning to the built-in data set rivers, it would be very useful if the rivers data set also had the names of the rivers also stored. That is, for each river, we would like to know both the name of the river and the length of the river. We might organize the data by having one column, titled river, that gave the name of the rivers, and another column, titled length, that gave the length of the rivers. This leads us to one of the most common data types in R, the Data Frame. A data frame consists of a number of observations of variables. Some examples would be:
- The name and length of major rivers.
- The height, weight, and blood pressure of a sample of healthy adult females.
- The high and low temperature in St Louis, MO, for each day of 2024.
Example 1.10 Let’s look at the data set mtcars, which is a predefined data set in R.
Start with str( mtcars ). You can see that mtcars consists of 32 observations of 11 variables. The variable names are mpg, cyl, disp and so on. You can also type ?mtcars on the console to see information on the data set. Some data sets have more detailed help pages than others, but it is always a good idea to look at the help page.
You can see that the data is from the 1974 Motor Trend magazine. You might wonder why we use such an old data set. In the R community, there are standard data sets that get used as examples when people create new code. The fact that familiar data sets are usually used lets people focus on the new aspect of the code rather than on the data set itself. In this course, we will do a mix of data sets; some will be up-to-date and hopefully interesting. Others will familiarize you with the common data sets that “developeRs” use.
The bracket operator [ ] picks out rows, columns, or individual entries from a data frame. It requires two arguments, a row and a column.
For example, the weight or wt column of mtcars is column 6, so to get the third car’s weight, use:
mtcars[ 3, 6 ]## [1] 2.32To pick out the third row of the mtcars data frame, leave the column entry blank:
mtcars[ 3, ]## mpg cyl disp hp drat wt qsec vs am gear carb
## Datsun 710 22.8 4 108 93 3.85 2.32 18.61 1 1 4 1To pick out the first ten cars, we could use mtcars[ 1:10 , ].
To form a new data frame called smallmtcars,
that only contains the variables mpg, cyl and qsec, we could use
smallmtcars <- mtcars[ , c( 1, 2, 7 ) ]. Referencing columns by name is also allowed, so smallmtcars <- mtcars[ , c( "mpg", "cyl", "qsec" )] works.
Selecting a single column from a data frame is very common, so R provides the $ operator to make this easier.
To produce a vector containing the weights of all cars, for example:
mtcars$wt## [1] 2.620 2.875 2.320 3.215 3.440 3.460 3.570 3.190 3.150 3.440 3.440 4.070
## [13] 3.730 3.780 5.250 5.424 5.345 2.200 1.615 1.835 2.465 3.520 3.435 3.840
## [25] 3.845 1.935 2.140 1.513 3.170 2.770 3.570 2.780Both mtcars[ , "wt"] and mtcars[ , 6] produce the same vector result. Indexing the resulting vector gives the third car’s weight:
mtcars$wt[ 3 ]## [1] 2.32As with vectors, providing a Boolean vector will select observations of the data that satisfy certain properties.
For example, to pull out all observations that get more than 25 miles per gallon, use mtcars[mtcars$mpg > 25,].
In order to test equality of two values, you use ==. For example, in order to see which cars have 2 carburetors, we can use mtcars[ mtcars$carb == 2, ].
Finally, to combine multiple conditions, you can use the vector logical operators & for and and |, for or.
As an example, to see which cars either have 2 carburetors or 3 forward gears (or both), we would use mtcars[ mtcars$carb == 2 | mtcars$gear == 3, ].
Users new to working with computer software that requires them to enter code into a terminal manually like we do with R may be a bit confused about the distinction between parentheses, ( ), and brackets, [ ]. In most students’ experience, these grouping symbols have been used interchangeably in their previous math coursework. However, R is very particular about every symbol that the user offers it. It is possible that students would be quite comfortable with the expression \(f(x)\), but may be perplexed if they saw it written as \(f[x]\). This will be our mental trick to remembering when to use parentheses.
We will always use parentheses following a function. As as example, earlier in Section 1.2, we saw the square root function which was utilized via sqrt().
We will use brackets when trying to access certain parts of vectors, where the entry in the brackets is only controlling the index of a vector, or of a data frame, where the argument(s) entered in the brackets prior to the comma control the rows of the data frame and the argument(s) entered after the comma control the columns. Revisit Sections 1.4.2 and 1.6 for further information.
We will later see the use of braces, { }, when we look to group chunks of R code together to run as one unit. We will first see this in Chapter 6
Example 1.11 The airquality data frame is part of base R, and it gives air quality measurements for New York City in the summer of 1973.
str( airquality )## 'data.frame': 153 obs. of 6 variables:
## $ Ozone : int 41 36 12 18 NA 28 23 19 8 NA ...
## $ Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
## $ Wind : num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
## $ Temp : int 67 72 74 62 56 66 65 59 61 69 ...
## $ Month : int 5 5 5 5 5 5 5 5 5 5 ...
## $ Day : int 1 2 3 4 5 6 7 8 9 10 ...From the structure, we see that airquality has 153 observations of 6 variables. The Wind variable is numeric and the others are integers.
We now find the hottest temperature recorded, the average temperature in June, and the day with the most wind:
max( airquality$Temp )## [1] 97junetemps <- airquality[ airquality$Month == 6, "Temp" ]
mean( junetemps )## [1] 79.1mostwind <- which.max( airquality$Wind )
airquality[ mostwind, ]## Ozone Solar.R Wind Temp Month Day
## 48 37 284 20.7 72 6 17It got to \(97^\circ\)F at some point, it averaged \(79.1^\circ\)F in June, and June 17 was the windiest day that summer.
1.7 Reading Data From Files
Loading data into R is one of the most important things to be able to do. If you can’t get R to load your data, then it doesn’t matter what kinds of neat tricks you could have done. It can also be one of the most frustrating things – not just in R, but in general. Your data might be on a web page, in an Excel spreadsheet, or in any one of dozens of other formats each with its own idiosyncrasies. R has powerful packages that can deal with just about any format of data you are likely to encounter, but for now we will focus on just one format, the CSV file. Usually, data in a CSV file will have the extension “.csv” at the end of its name. CSV stands for “Comma Separated Values” and means that the data is stored in rows with commas separating the variables. For example, CSV formatted data might look like this:
"Gender","Body.Temp","Heart.Rate"
"Male",96.3,70
"Male",96.7,71
"Male",96.9,74
"Female",96.4,69
"Female",96.7,62This would mean that there are three variables: Gender, Body.Temp and Heart.Rate. There are 5 observations: 3 males and 2 females. The first male had a body temperature of 96.3 and a heart rate of 70.
The command to read a CSV file into R is read.csv. It takes one argument, a string giving the path to the file on your computer.
R always has a working directory, which you can find with the getwd() command, and you can see with the Files tab in RStudio.
If your file is stored in that directory, you can read it with the command read.csv("mydatafile.csv").
If you want to load a CSV file that you have saved on your computer, you can run the following code chunk to bring up an interactive window where you can search for the file on your computer.
temp <- read.csv( file.choose() ) This will save the file as temp. You can either change the name of temp in the line above, or run the line below where you can change the file name on the left hand side shown as NewFileName below.
NewFileName <- tempExample 1.12 We will walk through how to open a .csv file that you found on the internet. We begin by downloading a file. You can downloading a dataset about US Presidents by clicking on the link below.
We can now load the file by running the following line of code.
temp <- read.csv( file.choose() )This should open a screen on your computer which will allow you to search for the file, USPresidents.csv. It is likely in your downloads folder if you successfully downloaded it.
It is now suggested that you rename the file to something more useful. We will call it USPresidents and achieve this via the following line of code.
USPresidents <- tempYou should now see a file called USPresidents in your Environment under Data. There is still a copy of the same dataset called temp on your computer as well. You can leave it on your machine and simply write over it each time you use this technique, or you can remove the extra copy now by running the following command which utilizes the remove function, rm().
rm( temp )If the CSV file that you want to read is hosted on a web page, it is sometimes easier to read the file directly from the web page by using a line like read.csv("http://website/file.csv").
Direct downloads like above will be the primary method used to open new datasets on Statypus.
Example 1.13 There is a csv hosted at https://statypus.org/files/hot_dogs.csv. To load it, use:
hot_dogs <- read.csv( "https://statypus.org/files/hot_dogs.csv" )Using functions we have looked at above, examine the dataset. What kind of data are in the file? The following remark may help.
We can’t emphasize enough the importance of looking at your data after you have loaded it. Start by using str(), head(), and summary() on your variable after reading it in. As often as not, there will be something you will need to change in the data frame before the data is usable.
To write R data frames to a CSV file, use the write.csv() command.
If your row names are not meaningful, then often you will want to add row.names = FALSE. The command write.csv( mtcars, "mtcars_file.csv", row.names = FALSE ) writes the variable mtcars to the file mtcars_file.csv.
1.8 Packages
When you first start using R, the commands and data available to you are called “Base R.” The R language is extensible, which means that over the years people have added functionality. New functionality comes in the form of a package, which may be included in your R distribution or which you may need to install. For example, the HistData package contains a few dozen data sets with historical significance.
Happily, installing packages is extremely simple: in RStudio you can click the Packages tab in the lower right panel, and then hit the Install button to install any package you need. Alternatively, you can use the install.packages command.
Example 1.14 In this example, we will install and investigate the package HistData
install.packages( "HistData" )Installing packages does require an Internet connection, and frequently when you install one package R will automatically install other packages, called dependencies, that the package you want must have to work.
Package installation is not a common operation. Once you have installed a package, you have it forever.14 However, each time you start R, you need to load any packages you want to use. You do this with the library command:
library( HistData )Once you have loaded the package, the contents of the package are available to use. HistData contains a data set DrinksWages with data on drinking and earned wages from 1910. After loading HistData you can inspect DrinksWages and learn that riveters were paid well in 1910:
head( DrinksWages )## class trade sober drinks wage n
## 1 A papercutter 1 1 24.00000 2
## 2 A cabmen 1 10 18.41667 11
## 3 A goldbeater 2 1 21.50000 3
## 4 A stablemen 1 5 21.16667 6
## 5 A millworker 2 0 19.00000 2
## 6 A porter 9 8 20.50000 17DrinksWages[ which.max( DrinksWages$wage ), ]## class trade sober drinks wage n
## 64 C rivetter 1 0 40 1Some packages are large, and you may only require one small part of them. The :: double colon operator selects the required object without loading the entire package. For example, MASS::immer can access the immer data from the MASS package without loading the large and messy MASS package:
head( MASS::immer )## Loc Var Y1 Y2
## 1 UF M 81.0 80.7
## 2 UF S 105.4 82.3
## 3 UF V 119.7 80.4
## 4 UF T 109.7 87.2
## 5 UF P 98.3 84.2
## 6 W M 146.6 100.4Learning statistics with R may require you to use a variety of packages. Though you need only install each package one time, you will need to use the :: operator or load it with library each time you start a new R session. One of the more common errors you will encounter is: Error: object 'so-and-so' not found, which may mean that so-and-so was part of a package you forgot to load.
1.9 Errors and Warnings
R, like most programming languages, is very picky about the instructions you give it. It pays attention to uppercase and lowercase characters, similar looking symbols like = and == mean very different things, and every bit of punctuation is important.
When you make mistakes (called bugs) in your code, a few things may happen: errors, warnings, and incorrect results. Code that runs but that runs incorrectly is usually the hardest problem to fix, since the computer sees nothing wrong with your code and debugging is left entirely to you.
Example 1.15 The simplest bug is when your code produces an error. Here are a few examples:
mean( primse )## Error in mean(primse): object 'primse' not foundmtcars[ , 100 ]## Error in `[.data.frame`(mtcars, , 100): undefined columns selectedairquality[ airquality$Month = 6 , "Temp" ]## Error in parse(text = input): <text>:1:30: unexpected '='
## 1: airquality[ airquality$Month =
## ^The first is a typical spelling error. In the second, we asked for column 100 of mtcars, which has only 11 columns. In the third, we used = instead of ==. You will encounter these sorts of errors all the time and then quickly graduate to much more subtle bugs.
Warnings occur when R detects a potential problem in your code but can continue working. For example, below we try to assign an entire vector to one element of a vector. R cannot do this, so it assigns the first element of the vector and prints a warning message.
a <- 1:10
a[ 5 ] <- 100:200## Warning in a[5] <- 100:200: number of items to replace is not a multiple of
## replacement lengthComplicated statistical operations such as hypothesis tests and regression analysis frequently produce warnings or messages that the user might not care about. The output of R commands in this book will sometimes omit these messages to save space and focus attention on the important part of the output. If you notice your command producing warnings not shown in the book, either ignore them or dig deeper and learn a little more about R. In your own code, you can use the commands suppressWarnings and suppressMessages to remove extraneous output for presentation quality work.
A pitfall that traps many beginning R users is the + prompt. If you are working in the console or running a line of code from an R script you may see a + instead of the friendly > prompt in the console. This means that the command you typed was incomplete; for example, because you opened a parenthesis ( and failed to close it with ). An example of this is shown below.
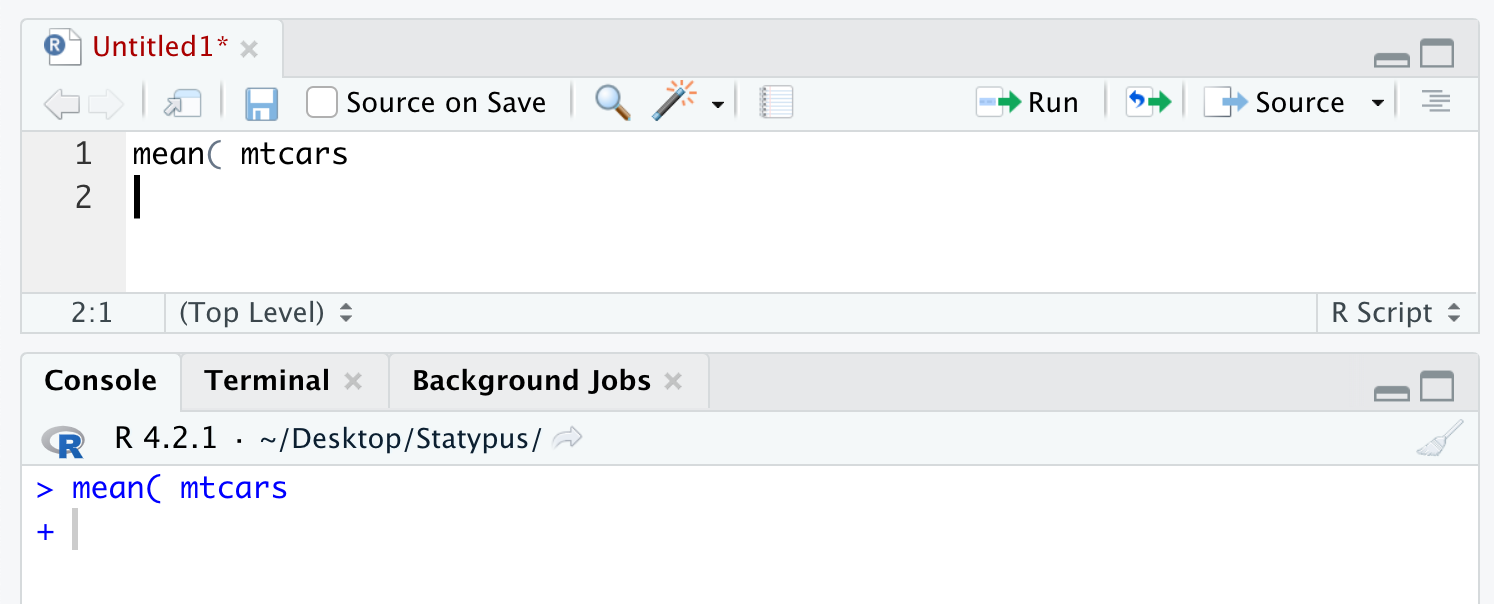
Figure 1.9: The Annoying + Prompt
Sometimes this behavior is desirable, allowing a long command to extend over two lines. More often, the + is unexpected. You can escape from this situation with the escape key, ESC, hence its name.
Review
Big Ideas
Section 1.2
You can’t get very far without storing results of your computations to variables! The way15 to do so is with the arrow <-. Typing Alt + - on a PC or option + - on a Mac are the keyboard shortcuts for <-, but you can also just use the < and - keys on your keyboard.
It is note that this is a directional operation. The line of code below would set the variable x to be the value 2 and it would then appear in the Upper Right panel of RStudio in your Environment.
x <- 2However, running the following line of code will cause an error (we will look at errors and warnings more in Section 1.9).
2 <- x## Error in 2 <- x: invalid (do_set) left-hand side to assignmentHere RStudio is telling us that we have tried to assign the value of x into the constant 2. This is nonsensical and R tells us just that.
This does allow us to write some lines of code that would be paradoxical if we used an equal sign. For example consider the following line of code.
x <- x + 1This line of code takes the existing value of x, adds 1 to it, and then stores it back into the variable x. This is another example of code that would not work if we switched the x and x+1.16
If you find that a dataset or value such as pi is not acting as you expect and you want to have them return to the default state, you have a couple of choices. You can restart R by clicking on Session in the top row menu and then selecting Restart as shown bloew.

Figure 1.10: How To Restart RStudio Session
This will do more than just reset variables to their default values; it will reset R to its start-up state. If you think you may have messed something up, this is a quick way to “start again.”
You can also remove an object from the R environment by using the function remove function, rm(). The function rm accepts the name of an object and removes it from memory. As an example, look at the code below:
pi## [1] 3.141593pi <- 3.2
pi## [1] 3.2rm( pi )
pi## [1] 3.141593If you begin typing (at least the first three characters of) something into RStudio, auto-complete will search for all things in memory, data or functions, in a non-case-sensitive way and allow you to choose from a drop down list. For example, typing vie into an R script or into the R console it will pop up a menu to allow you to choose the function, View(), as shown below.

Figure 1.11: Autocomplete Example
If there are more than one option for the three characters for what you type, you get a dropdown showing all of the objects that begin with that regardless of case. For example, below is what you will likely see if you type in bas into R.

Figure 1.12: Autocomplete Example
At Statypus, we call this the Rule of Type Three: that is, you should type the first three characters of the element you are looking for and then using the menu to select the appropriate value.
Section 1.3
R comes with built-in help. In RStudio, there is a help tab in the lower right panel. Placing a ? before an object gives help for that object.
Section 1.4
Observe the use of > for comparison in Example 1.6. In R (and most modern programming languages), there are some fundamental comparison operators:
==equal to!=not equal to>greater than<less than>=greater than or equal to<=less than or equal to
Another important operator is the %in%, which is TRUE if a value is in a vector. For example:
4 %in% primes## [1] FALSEodds <- seq( from = 1 , to = 11 , by = 2 )
primes[ primes %in% odds ]## [1] 3 5 7 11In Example 1.8 we ran the following line of code: sort( discoveries, decreasing = TRUE ). This is an example of running an R function and shows the basic syntax we will use, which is shown below.
function( argument1, argument2 )In R, functions can have more than input, we show 2 above, but it can be more. Functions can also have more than one output. This may go against the definition of a function that you learned, but the most important concept is still true. The output of a function is uniquely determined by the arguments that we pass to the function.17
We can see what arguments a function wants by typing in the function, such as sort(), into an R script (or in the Console) and waiting. A yellow pop-up will appear showing the arguments that the function needs passed to it.

Figure 1.13: The pop-up showing the arguments of sort()
This shows that the main arguments are x, the data to be sorted, and decreasing which is set to FALSE by default as indicated in the pop-up. The ellipsis indicates that there are other, and lesser used, arguments which we can look at by using the help option by running ?sort.
Section 1.6
Users new to working with computer software that requires them to enter code into a terminal manually like we do with R may be a bit confused about the distinction between parentheses, ( ), and brackets, [ ]. In most students’ experience, these grouping symbols have been used interchangeably in their previous math coursework. However, R is very particular about every symbol that the user offers it. It is possible that students would be quite comfortable with the expression \(f(x)\), but may be perplexed if they saw it written as \(f[x]\). This will be our mental trick to remembering when to use parentheses.
We will always use parentheses following a function. As as example, earlier in Section 1.2, we saw the square root function which was utilized via sqrt().
We will use brackets when trying to access certain parts of vectors, where the entry in the brackets is only controlling the index of a vector, or of a data frame, where the argument(s) entered in the brackets prior to the comma control the rows of the data frame and the argument(s) entered after the comma control the columns. Revisit Sections 1.4.2 and 1.6 for further information.
We will later see the use of braces, { }, when we look to group chunks of R code together to run as one unit. We will first see this in Chapter 6
Important Alerts
Section 1.2
It is important to choose your variable names wisely. Variables in R cannot start with a number, and for our purposes, they should not start with a period.
Do not use T or F as a variable name. Think twice before using c, q, t, C, D, or I as variable names, as they are already defined.
It may also be a bad idea (and is one of the most frustrating things to debug on the rare occasions that it causes problems) to use sum, mean, or other commonly used functions as variable names. T and F are variables with default values TRUE and FALSE, which can be changed.
We recommend writing out TRUE and FALSE rather than using the shortcuts T and F for this reason.**
Section 1.8
Learning statistics with R may require you to use a variety of packages. Though you need only install each package one time, you will need to use the :: operator or load it with library each time you start a new R session. One of the more common errors you will encounter is: Error: object 'so-and-so' not found, which may mean that so-and-so was part of a package you forgot to load.
Section 1.9
A pitfall that traps many beginning R users is the + prompt. If you are working in the console or running a line of code from an R script you may see a + instead of the friendly > prompt in the console. This means that the command you typed was incomplete; for example, because you opened a parenthesis ( and failed to close it with ). An example of this is shown below.

Figure 1.14: The Annoying + Prompt
Sometimes this behavior is desirable, allowing a long command to extend over two lines. More often, the + is unexpected. You can escape from this situation with the escape key, ESC, hence its name.
Important Remarks
Section 1.1
Throughout the book, lines that start with ## indicate output from R commands. These will not show up when you type in the commands yourself. The [1] in Example 1.1 below (and likely all R output in the book) indicate that there is one piece of output from the command. These will show up when you type in the commands.
Section 1.2
Throughout the book, lines that start with ## indicate output from R commands. These will not show up when you type in the commands yourself. The [1] in Example 1.1 (and likely all R output in the book) indicate that there is one piece of output from the command. These will show up when you type in the commands.
R is a functional programming language. If you don’t know what that means, that’s OK, but as you might guess from the name, functions play a large role in R. We will see many, many functions throughout the book. Every time you see a new function, think about the following four questions:
- What type of input does the function accept?
- What does the function do?
- What does the function return as output?
- What are some typical examples of how to use the function?
Many typos can be avoided by following the Rule of Type Three as R is case-sensitive so that view( rivers ) causes an error while View( rivers ) will display the vector rivers in the upper left panel of RStudio.
view( rivers )## Error in view(rivers): could not find function "view"Section 1.3
It can take some time to get used to reading R Documentation. For now, we recommend reading the four headings discussed in Example 1.3 to see whether there are things you can learn about new functions. Don’t worry if there are things in the documentation that you don’t yet understand.
Section 1.4
The expression [16] on the second line of the last output of Example 1.5 tells us that 8.5 is the 16th value (out of the 21 determined by length.out) of the vector.
Section 1.7
We can’t emphasize enough the importance of looking at your data after you have loaded it. Start by using str(), head(), and summary() on your variable after reading it in. As often as not, there will be something you will need to change in the data frame before the data is usable.
Exercises
Exercises 1.1 – 1.7 require material through Sections 1.2 – 1.4.
Exercise 1.1 Let x <- c( 1, 2, 3 ) and y <- c( 6, 5, 4 ). Predict what will happen when the following pieces of code are run. Check your answer.
x * 2x * yx[1] * y[2]
Exercise 1.2 Let x <- c( 1, 2, 3 ) and y <- c( 6, 5, 4 ). What is the value of x after each of the following commands? (Assume that each part starts with the values of x and y given above.)
x + xx <- x + xy <- x + xx <- x + 1
Exercise 1.3 Determine the values of the vector vec after each of the following commands is run.
vec <- 1:10vec <- 1:10 * 2vec <- 1:10^2vec <- 1:10 + 1vec <- 1:(10 * 2)vec <- rep( c( 1, 1, 2 ), times = 2 )vec <- seq( from = 0, to = 10, length.out = 5 )
Exercise 1.4 In this exercise, you will graph the function \(f(p) = p(1-p)\) for \(p \in [0,1]\).
- Use
seqto create a vectorpof numbers from 0 to 1 spaced by 0.2. - Use
plotto plotpin thexcoordinate andp * ( 1 - p )in theycoordinate. Read the help page forplotand experiment with thetypeargument to find a good choice for this graph. - Repeat, but with creating a vector
pof numbers from 0 to 1 spaced by 0.01.
Exercise 1.5 Use R to calculate the sum of the squares of all numbers from 1 to 100: \(1^2 + 2^2 + \dotsb + 99^2 + 100^2\).
Exercise 1.6 Let x be the vector obtained by running the R command x <- seq( from = 10, to = 30, by = 2 ).
- What is the length of
x? (By length, we mean the number of elements in the vector. This can be obtained using thestrfunction or thelengthfunction.) - What is
x[2]? - What is
x[1:5]? - What is
x[1:3*2]? - What is
x[1:(3*2)]? - What is
x > 25? - What is
x[x > 25]? - What is
x[-1]? - What is
x[-1:-3]?
Exercise 1.7 R has a built-in vector rivers which contains the lengths of major North American rivers.
- Use
?riversto learn about the data set. - Find the mean and standard deviation of the rivers data using the base R functions
meanandsd. - Make a histogram, using the
histfunction, of the rivers data. - Get the five number summary, using the
summaryfunction, of rivers data. - Find the longest and shortest lengths of rivers in the set.
- Make a list of all (the lengths of) rivers longer than 1000 miles.
Exercises 1.8 – 1.11 require material through Sections 1.5 – 1.6.
Exercise 1.8 Consider the built-in data frame airquality.
- How many observations of how many variables are there?
- What are the names of the variables?
- What type of data is each variable?
- Do you agree with the data type that has been given to each variable? What would have been some alternative choices?
Exercise 1.9 There is a built-in data set state, which is really seven separate variables with names such as state.name, state.region, and state.area.
- What are the possible regions a state can be in? How many states are in each region?
- Which states have area less than 10,000 square miles?
- Which state’s geographic center is furthest south? (Hint: use
which.min)
Exercise 1.10 Consider the mtcars data set.
- Which cars have 4 forward gears?
- What subset of
mtcarsdoesmtcars[ mtcars$disp > 150 & mtcars$mpg > 20, ]describe? - Which cars have 4 forward gears and manual transmission? (Note: manual transmission is 1 and automatic is 0.)
- Which cars have 4 forward gears or manual transmission?
- Find the mean mpg of the cars with 2 carburetors.
Exercise 1.11 Consider the mtcars data set.
- Convert the
amvariable to a factor with two levels,autoandmanual, by typing the following:mtcars$am <- factor(mtcars$am, levels = c(0, 1), labels = c("auto", "manual")). - How many cars of each type of transmission are there?
- How many cars of each type of transmission have gas mileage estimates greater than 25 mpg?
You can undo the change made to mtcars by running the line rm(mtcars) in your console or through an R script. In general, it is likely a good idea to create a “working copy” of a data set if you are wanting to modify it in any significant way. In this case, we could have first ran mtcars2 <- mtcars and then ran mtcars2$am <- factor(mtcars2$am, levels = c(0, 1), labels = c("auto", "manual")). For more information on the factor function, see ?factor.
Exercises 1.12 – 1.13 require material through Section 1.8.
Exercise 1.12 This problem uses the data set hot_dogs. See Example 1.13 if needed.
- How many observations of how many variables are there? What types are the variables?
- What are the three kinds of hot dogs in this data set?
- What is the highest sodium content of any hot dog in this data set?
- What is the mean calorie content for Beef hot dogs?
Exercise 1.13 This problem uses the data set DrinksWages from the package HistData, see Example 1.14 if needed.
- How many observations of how many variables are there? What types are the variables?
- The variable
wagecontains the average wage for each profession. Which profession has the lowest wage? - The variable
ncontains the number of workers surveyed for each profession. Sum this to find the total number of workers surveyed. - Compute the mean wage for all workers surveyed by multiplying
wagebynfor each profession, summing, and then dividing by the total number of workers surveyed.
Shaw, George; Nodder, Frederick Polydore (1799). “The Duck-Billed Platypus, Platypus anatinus”. The Naturalist’s Miscellany. 10 (CXVIII): 385–386↩︎
The value \(\frac{\pi^2}{6}\) may look unnatural to some and that is to be expected. The Basel Problem was solved by one of the smartest mathematicians to ever lived, Leonhard Euler, in 1734 and involved evaluating a sum which ended up equaling exactly \(\frac{\pi^2}{6}\).↩︎
Using
=for variable assignment is also allowed, as in many other programming languages. The arrow was the original and only assignment operator in R until 2001, and arrow is required by the Google and Tidyverse R style guides. However, some R users prefer to use=, and it is one of those things that you just can’t reason about. The Stack Overflow question, “What are the differences between=and<-in R?” has over 393K views as of this writing.↩︎It is possible to reverse the direction of the arrow operator to create a “Right” arrow.
->, but for simplicity’s sake, we will solely use the “Left” arrow<-here on Statypus.↩︎Perhaps to 3.2, if you are Edward J. Goodwin trying to enact the “Indiana Pi Bill.”↩︎
One may argue that some of the “random” functions we will use, such as
sample()andrnorm, violate this concept. However, this is not the case as these functions also call on a “hidden” argument which is the “seed” it uses to create what we infer as a random value. The user can use theset.seed()function to choose the seed value prior to running a random function and the results will be consistent. This is especially useful when doing something such as writing a textbook when you want to be able to discuss the results of a function and not have it change when you recompile the book.↩︎L stands for “long,” a reference to the number of bits used to store R integers.↩︎
Well, at least until you update R to the newest version, which cleans out the packages that you had previously installed.↩︎
Using
=for variable assignment is also allowed, as in many other programming languages. The arrow was the original and only assignment operator in R until 2001, and arrow is required by the Google and Tidyverse R style guides. However, some R users prefer to use=, and it is one of those things that you just can’t reason about. The Stack Overflow question, “What are the differences between=and<-in R?” has over 393K views as of this writing.↩︎It is possible to reverse the direction of the arrow operator to create a “Right” arrow.
->, but for simplicity’s sake, we will solely use the “Left” arrow<-here on Statypus.↩︎One may argue that some of the “random” functions we will use, such as
sample()andrnorm, violate this concept. However, this is not the case as these functions also call on a “hidden” argument which is the “seed” it uses to create what we infer as a random value. The user can use theset.seed()function to choose the seed value prior to running a random function and the results will be consistent. This is especially useful when doing something such as writing a textbook when you want to be able to discuss the results of a function and not have it change when you recompile the book.↩︎