Chapter 6 From Proportions to Probabilities

Figure 6.1: Statypus Playing Dice

The platypus only naturally exists along the coast of Eastern Australia. In fact, the only place that a platypus can be found outside of Australia is at the San Diego Zoo Safari Park. They are best friends with the giant pandas that live there as well! (The last statement is false, but I wish it was true.)³⁸

The goal of probability and statistics is to understand the real world. Many of the situations we face on a daily basis involve a certain amount of chance. The time it takes to drive to the store can greatly be affected by the amount of traffic on the roads or simply the timing of the traffic signals along your path. Modern cell phones are incredibly resilient, but every drop offers the chance that it may break or become damaged. Even our births have an element of chance as certain proportions of people are born with life threatening conditions, such as trisomy 13, based on random genetic “mistakes” made while duplicating the genetic code.

probability experiments in the real world are usually slow and often expensive. Instead of running real world experiments, it is easier to model these experiments and then use a computer to imitate the results. This process goes by several names, such as stochastic simulation, Monte Carlo simulation or probability simulation. Since this is the only type of simulation we will discuss, we simply call it simulation.

New R Functions Used

All functions listed below have a help file built into RStudio. Most of these functions have options which are not fully covered or not mentioned in this chapter. To access more information about other functionality and uses for these functions, use the ? command. E.g. To see the help file for replicate``, you can run?replicateor?replicate()` in either an R Script or in your Console.

sample(): Takes a sample of the specified size from the elements of x using either with or without replacement.
replicate(): Allows for repeated evaluation of an expression (which will usually involve random number generation).
anyDuplicated(): Determines which elements of a vector or data frame are duplicates of elements with smaller subscripts.
cumsum(): Returns a vector whose elements are the cumulative sums of the elements of the argument.
rle(): Run Length Encoding: Computes the lengths and values of runs of equal values in a vector.

Remark. The functions cumsum() and rle() are only used in the challenging bonus problems and do not have any explanation here. Use ?cumsum or ?rle in your RStudio Console for help with these.

6.1 Proportion or Probability?

Games of chance are a staple of childhood and allow players of different ages to compete fairly. Games such as “Candy Land” require no skill as there is no strategy that can be employed to gain an advantage. Games such as “Snakes and Ladders” are even more complex, but again the outcome of the game is completely determined by the instrument of chance, a single six sided die. However, not all 6 sided dice are created equally.

Pass the Pigs Dice, Photo by [Larry D. Moore](https://commons.wikimedia.org/wiki/File:Pass_the_pigs_dice.jpg)

Figure 6.2: Pass the Pigs Dice, Photo by Larry D. Moore

“Pass the Pigs”³⁹ is a version of the classic dice game called “Pig,”⁴⁰ but it uses asymmetric dice in the shape of pigs. The result of throwing a single pig can result in 6 distinct results just like that of a standard die. However, unlike a standard die, the chance of each result is definitely not equal. Dr. John Kerr of Duquesne University published a paper in the Journal of Statistics Education⁴¹ in 2006 about the advanced statistical models which can be modeled by the game. We, however, are only concerned with understanding the basic distribution of the outcomes of rolling a single pig. We begin by downloading a slightly modified version of Dr. Kerr’s data.

Pigs <- read.csv( "https://statypus.org/files/Pigs.csv" )

We can get a quick look at the dataset with the str function.

str(Pigs)

## 'data.frame':    5977 obs. of  5 variables:
##  $ black : chr  "Razorback" "Trotter" "Razorback" "Trotter" ...
##  $ pink  : chr  "Dot Up" "Razorback" "Razorback" "Dot Up" ...
##  $ score : int  5 10 20 5 10 5 5 10 5 10 ...
##  $ height: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ start : int  0 0 0 0 0 0 0 0 0 0 ...

To fully understand all of the data in this data frame, a discussion of the data and the work done on it can be found at the following link.

https://statypus.org/files/PigDictionary.txt

However, we will only be focused on the column labeled black. This is the result of the “rolls” of the pig with a black mark on its snout. We start our investigation of the distribution of rolling a pig by looking at a table of the values.

table( Pigs$black )

## 
##       Dot Down         Dot Up Leaning Jowler      Razorback        Snouter        Trotter 
##           2063           1796             29           1354            184            551

To get a visual representation of this table, we will sort the data and construct a barplot.

par( mar = c( 8, 4, 0, 0 ) )    
#The above is used to ensure that the names of the rolls are not cut off.
#The option `las = 2` is used to orient the names vertically.
barplot( sort( table( Pigs$black ), decreasing = TRUE ), las = 2 )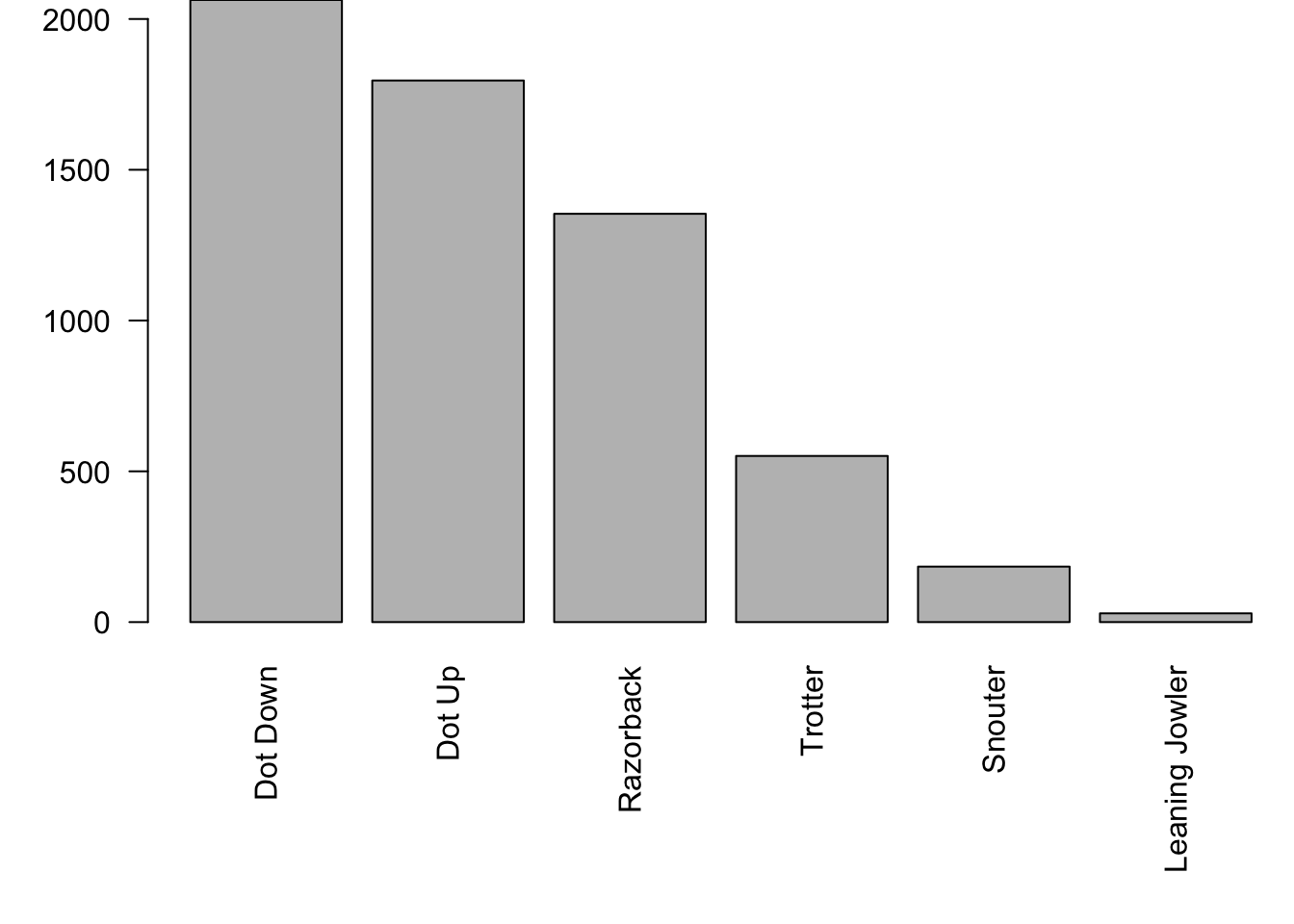

Figure 6.3: Frequency Bar Plot of Pig Rolls

While it is easy to see the relative differences of the outcomes above, using the proportions function will tell us the relative frequency of each outcome which will lead us towards the topic of this chapter, probability.

par( mar=c(8, 4, 0, 0) )
#The above is used to ensure that the names of the rolls are not cut off.
#The option `las = 2` is used to orient the names vertically.
barplot( sort( proportions( table( Pigs$black ) ), decreasing = T ), las =2 )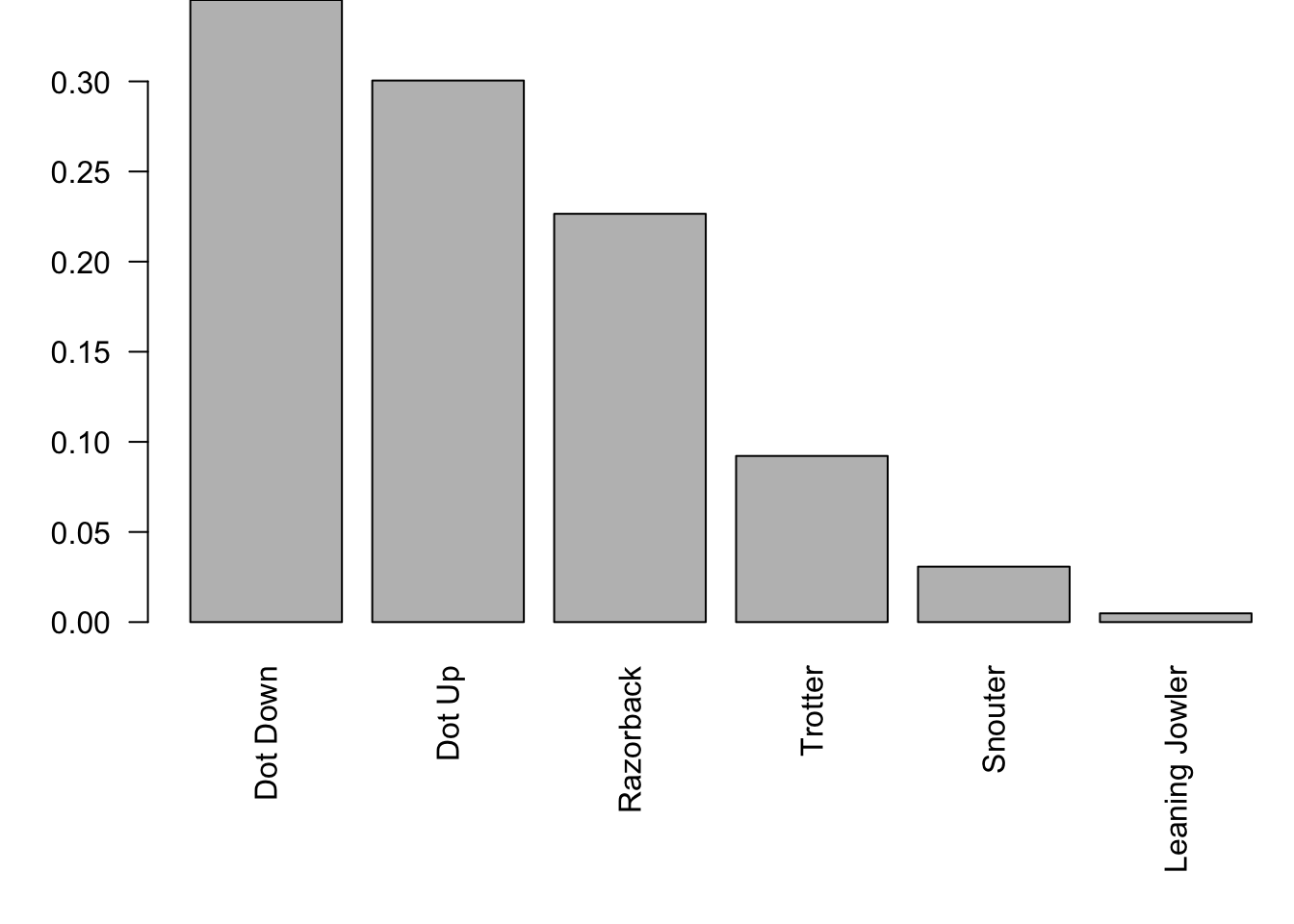

Figure 6.4: Relative Frequency Barplot of Pig Rolls

Now suppose you were handed the pig with the black dot on its snout and you wanted to know what the probability that the next roll would result in “Dot Up.”

Based on the barplot above, the proportion of the rolls in our dataset resulted in “Dot Up” was approximately 30%. However, is that the same as the probability of the next roll?⁴²

The concepts of proportion and probability may be a bit intertwined for some readers and this is with good cause. Consider the following question.

What proportion of students at your school are female?

This is asking the exact same thing as the following question.

If a random student at your school is selected, what is the probability that they are female?

That is, we can ask the same question about the proportion of things that are or ask about the probability that something will be.

In fact, once we have the Law of Large Numbers, Theorem 6.1, we will be able to say that after a large number of observations, it is basically impossible to distinguish between proportions and probabilities.

This setup was done to offer an example of a Probability Experiment before we formally defined it. We will now give the formal definition.

Definition 6.1 A Probability Experiment is the running of one or more Trials that each results in an Outcome. A collection of outcomes is called an Event and the collection of all outcomes is called the Sample Space. If $E$ is an event, we use the notation $P(E)$ to be the probability that a trial will result in the event $E$.

Example 6.1 The rolling of a single pig from the game of “Pass the Pigs” is an example of a probability experiment. In this case, we have

\[ S = \left\{ \text{Dot Up},\; \text{Dot Down},\; \text{Razorback},\; \text{Trotter},\; \text{Snouter},\; \text{Leaning Jowler} \right\}\] where each element of $S$ is an outcome. An example of an event which is not an outcome would be what we can call a “Sider” which is either Dot Down or Dot Up. That is, formally, we would have

\[\text{Sider} = \left\{ \text{Dot Down},\; \text{Dot Up} \right\}.\]

While we do indeed have the notion of a probability experiment, we haven’t even mentioned the concept of probability which was also present in the definition. To get an idea of what rules probability should follow, we look at the properties that proportions follow. To get a quick feel, we can look at the proportions of the rolls for the black pig (rounded to 4 decimal places).

round( sort( proportions( table( Pigs$black )), decreasing = TRUE ), 4 )

## 
##       Dot Down         Dot Up      Razorback        Trotter        Snouter Leaning Jowler 
##         0.3452         0.3005         0.2265         0.0922         0.0308         0.0049

It is clear that proportions should be values between 0 and 1 and that they should add up to 1. We use this as a basis to extend the definition of a probability experiment with what we call the Rules of Probability.

Definition 6.2 (The Rules of Probability) The probabilities of events in the sample space, $S$, of a probability experiment must satisfy the following:

$0 \leq P(E) \leq 1$ for all events $E$.
$P( a \text{ does not happen }) = 1 - P(a)$ for all outcomes $a \in S$
$P(a \text{ or } b ) = P(a) + P(b)$ for all distinct outcomes $a$ and $b$
If $S$ is finite, $\displaystyle{ \sum_{a \in S } P(a) = 1 }$ where $a$ is taken over all outcomes in $S$

Example 6.2 We can fully realize the rolling of a pig as a probability experiment by assigning probabilities that satisfy Definition 6.2. Let the following table give the probability of $P(a)$ for each of the outcomes $a \in S$:

## 
##       Dot Down         Dot Up      Razorback        Trotter        Snouter Leaning Jowler 
##         0.3452         0.3005         0.2265         0.0922         0.0308         0.0049

Using the Rules of Probability, we can also find the following facts.

Each value in the table satisfies $0 \leq P(a) \leq 1$
$P( \text{not a Razorback} ) = 1 - P(\text{Razorback}) = 1 - 0.2265 = 0.7735$
$P(\text{Sider}) = P(\text{Dot Down or Dot Up}) = P(\text{Dot Down}) + P(\text{Dot Up}) = 0.3452 + 0.3005$

Remark. The very careful reader likely realized that we didn’t check that the sum of the probabilities was equal to 1. If you do check this, you will see that the probabilities is 1.0001. This is not a violation of Definition 6.2, but instead, just a consequence of us rounding rational numbers to only four decimal places. The following calculation shows that the sum of the probabilities would be 1 if we hadn’t rounded.

sum( proportions( table( Pigs$black ) ) )

## [1] 1

6.2 Random Variables

Real world data displays variation among observations. As such, if we want to reasonably predict the behavior of data, we need to not only understand the most typical value it may take on, we must also understand how often it will take on other values. That is, we need to understand the probability that an observation takes on the possible values of the dataset. Because the values vary, we will look at how we can use the concept of a Random Variable to understand the variability in real world scenarios.

Definition 6.3 Given a probability experiment with a sample space, $S$, we define a Random Variable, $X$, to be a rule that assigns a real number to every outcome in $S$. If $S$ is already made up of real numbers, the rule is simply to let the random variable be equal to the outcome.

Example 6.3 In the case of Pass the Pigs, or rolling a single pig to be more precise, the random variable would be the following rule:

\[\begin{align*} \text{Dot Down} &\rightarrow 1\\ \text{Dot Up} &\rightarrow 2\\ \text{Razorback} &\rightarrow 3\\ \text{Trotter} &\rightarrow 4\\ \text{Snouter} &\rightarrow 5\\ \text{Leaning Jowler} &\rightarrow 6. \end{align*}\] We would now have the following facts about the new random variable:

\[\begin{align*} P(\text{Dot Down}) &= P( X =1)\\ P(\text{not a Trotter}) &= P(X \neq 4)\\ P(\text{Sider}) &= P(\text{Dot Down or Dot Up})\\ {} &= P(X = 1 \text{ or } X= 2) = P(X=1) + P(X=2) \end{align*}\]

Example 6.4 If we buy a two pound bag of potatoes, we could setup a probability experiment that counts the number of potatoes in the bag and let the random variable be the same number.

Remark. For any value, $x_\emptyset$, that a random variable does not actually ever equal, we set $P( X = x_\emptyset) = 0$.

Definition 6.4 A Discrete Random Variable is a random variable, $X$, that takes on values among the whole numbers, $\left\{ 0, 1, 2, 3, \ldots \right\}$.

Remark. We could define discrete random variables in a way to allow them to take on values in the negative integers or any other discrete⁴³ set. However, mathematically, what we have done is equivalent and will allow us to keep discrete random variables in the realm of “counting” things.

Definition 6.5 Given a discrete random variable, $X$, with possible outcomes given by $S$, we can define the Population Mean of $X$, denoted $\mu_X$, to be

\[\mu_X = \sum_{x\in S} \big( x \cdot P(X = x)\big).\] We can further define the Population Standard Deviation of $X$, denoted $\sigma_X$, to be \[\sigma_X = \sqrt{\sum_{x\in S} \big( \left(x - \mu_X\right)^2 \cdot P(X = x)\big)}.\]

Remark. The value $\mu_X$ is sometimes called the Expected Value of $X$ and denoted by $E[X]$. We will illustrate the motivation behind this with the following example.

Example 6.5 (Parameters of a Single Dice) Consider a “fair” 6-sided die, i.e. a die where $P(X = n) = \frac{1}{6}$ for each $n = 1,2, \ldots, 6$. We can calculate $\mu_X$ and $\sigma_X$ using Definition 6.5 as follows.

Dice <- 1:6
Dice

## [1] 1 2 3 4 5 6

This gives us all the values of $X$. As each probability is the same, we can simply multiply this vector by $\frac{1}{6}$.

Dice * 1/6

## [1] 0.1666667 0.3333333 0.5000000 0.6666667 0.8333333 1.0000000

The last step is to simply find the sum of this new vector.

sum( Dice * 1/6 )

## [1] 3.5

This says that the average roll of a die is 3.5. Of course, it is impossible to roll a 3.5, but if you rolled a large number⁴⁴ of times, we expect that the average of all our rolls to be 3.5.

If we were playing a game where the value on the die was our score, we should expect to score 3.5 points with each roll. This is why we also call $\mu_X$ the expected value.

We also note that the mean function built into R can do this immediately.

mean( Dice )

## [1] 3.5

We can continue on to $\sigma_X$ now that we have $\mu_X = 3.5$. We first find the values of $(x - \mu_X)^2$.

(Dice - 3.5)^2

## [1] 6.25 2.25 0.25 0.25 2.25 6.25

We now multiply by $\frac{1}{6}$ and then the square root of the sum to get $\sigma_X$.

sqrt( sum( (Dice - 3.5)^2 * 1/6 ))

## [1] 1.707825

One might expect this to match the sd function we introduced in Chapter 4, but that isn’t the case.

sd( Dice )

## [1] 1.870829

The reason for this is the fact that sd measures the sample standard deviation and we want the population standard deviation. We need to use the formula given in Section 4.2.5. We can borrow the code used in Example 4.8 and get the following

x <- Dice                                
sd( x ) * sqrt( ( length( x ) - 1 ) / length( x ) )

## [1] 1.707825

or we could use the function, popSD, that we developed then as well. [You may need to load the function using the “New Function” box found in Section 4.2.5.]

popSD( Dice )         #You may need to load popSD first.

## [1] 1.707825

This matches our manual calculation (and restores our faith in R). With a bit more care, we could workout that the exact representation of $\sigma_X$ is $\sqrt{\frac{35}{12}}$ which we “verify” by finding its approximation.

sqrt( 35 /12 )

## [1] 1.707825

Find the population mean and population standard deviation for a fair coin. That is, let

\[ \text{Heads} \rightarrow 1\] and \[ \text{Tails} \rightarrow 0.\] Assuming that $P(X = 0) = P(X = 1) = \frac{1}{2}$, find $\mu_X$ and $\sigma_X$.

6.3 Probabilities Via Simulation

In Section 6.1, we defined the probability of the different outcomes for rolling a pig based off of six thousand actual rolls⁴⁵ of a little physical pig. This is tied to what is called the Frequentist View of Probability where we look at probabilities as the relative frequency that events happen over the long run. This likely contrasts to the types of probabilities you may have studied before where we simply assumed that “all outcomes are equally likely” in cases such as flipping a coin or rolling a standard six-sided die. Outside of a classroom, it is unlikely to be able to have much confidence that any situation is perfect enough to assume that “all outcomes are equally likely” and we are better off looking at what happens over the long run in a large number of trials.

Theorem 6.1 (Law of Large Numbers) The Law of Large Numbers (LLN) states that the observed relative frequency of an event may not equal the true probability over a small number of trials. However, as the number of trials increases, the relative frequency of an event will⁴⁶ get closer and closer to the true probability.

In situations like a coin, we have a theoretical probability that we can use the LLN to compare to observed relative frequencies. However, in the case of situations like Pass the Pigs, we do not have any sense of how to find a theoretical value of $P(\text{Trotter})$. However, we can use the Law of Large Numbers to actually get an estimate of the “true” probability of a Trotter. That is to say, if we use a large number of trials, we can assume that the observed relative frequency of an outcome is close to its true probability.⁴⁷

What the Law of Large Number is loosely saying is that if we are looking at a large number of observations that the observed proportions and the “true” probabilities are basically the same. In fact, we can use a large number of observations to determine an estimate of a “true” probability if we are unable to find it with other techniques.

This means that the probabilities we defined for the pigs in Example 6.2 were indeed good estimates of the “unknowable true probabilities” of each outcome for rolling a pig.

Thus, to get a good estimate of a probability where we do not have a theoretical understanding of, we simply need to repeat the experiment a large number of times. While practical experiments such as the six thousand rolls of a pig are tangible and understandable, they are time consuming human beings are prone to recording errors over such a large number of trials. However, the rise of computational power now allows us to do repeated trials of some probability experiments with the precision and repeatability of a machine.

Definition 6.6 A Simulation is the use of computers to run theoretical trials of a probability experiment.

This section uses simulation as the center of a study of probability. With a good understanding of how to simulate experiments, you can answer a wide range of questions involving probability. Simulation also plays a fundamental role in modern statistical methods such as resampling, bootstrapping, non-parametric statistics, and genetic algorithms.

6.3.1 Probabilities with `sample`

We first used the R function sample() when finding a SRS in Chapter 2, but we now wish to leverage the function even further. For an experiment with a finite sample space $S =\{x_1, x_2, \ldots, x_n\}$, sample() can simulate one or many trials of the experiment. Essentially, sample treats $S$ as a bag of outcomes, reaches into the bag, and picks one.

The syntax of sample is

sample( x , size , replace , prob )

where the parameters are:

x: The vector of elements from which you are sampling.
size: The number of samples you wish to take.
replace: Whether you are sampling with replacement or not. Sampling without replacement means that sample will not pick the same value twice, and this is the default behavior. Pass replace = TRUE to sample if you wish to sample with replacement.
prob: A vector of probabilities or weights associated with x. It should be a vector of non-negative numbers of the same length as x.

Remark. If the sum of prob is not 1, it will be normalized. That is, each value in prob will be taken to be out of the sum of prob. For example, if the values in prob were 0.2, 0.3, and 0.4, then the actual probabilities would be 0.2/0.9 = 2/9, 0.3/0.9 = 1/3, and 0.4/0.9 = 4/9. If prob is not provided, then each element of x is considered to be equally likely.

The most straightforward use of sample is to choose one element of a vector “at random” like we did in Section 2.5.1.1. When people say “at random,” they usually mean that all outcomes are equally likely to be chosen, and that is how sample operates unless you tell it otherwise. To get a random integer from 1 to 10 we can use the code:

sample( x = 1:10 , size = 1 )

## [1] 1

You can copy and paste this code into your RStudio Console, or preferably, into an R Script. Your computer will likely give you a different number and if you run the code again, you will likely get a different number.

The size argument tells sample how many random numbers you want:

sample( x = 1:10 , size = 8 )

## [1]  4 10  6  5  9  1  3  7

Observe that the eight numbers chosen are all different. If you run this code on your own computer, you will almost certainly get a different string of numbers.

The replace argument of sample determines whether sample is allowed to repeat values. The name “replace” comes from the model that sample has a bag of outcomes and is reaching into the bag to draw one. When replace = FALSE, the default, once sample chooses a value from the bag of outcomes it won’t replace it into the bag. For example, above when the first value of sample was 4, the following draw cannot be 4. With replace = TRUE, sample draws an outcome from the bag, records it, and then puts it back into the bag.

Here we set replace = TRUE to get 20 random numbers from 1 to 10 which will necessarily have to have repeat values:

sample( x = 1:10 , size = 20 , replace = TRUE )

##  [1]  3  3 10  2  6  5  4  6  9 10  5  3  9  9  9  3  8 10  7 10

The prob argument of sample allows for sampling when outcomes are not all equally likely. We will illustrate this with a bloody example.

Example 6.6 (Looking at Blood Types) In the United States, human blood comes in four types: $O$, $A$, $B$, and $AB$. These types occur with the following probability distribution:

\[\begin{array}{lcccc} \text{Type} & A & AB & B &O\\ \text{Probability} & 0.40 & 0.04 & 0.11 & 0.45 \end{array}\]

We can sample thirty blood types from this distribution by defining a vector of blood types and a vector of their probabilities:

bloodtypes <- c("O", "A", "B", "AB")
bloodprobs <- c(0.45, 0.40, 0.11, 0.04)
sample(x = bloodtypes, size = 30, prob = bloodprobs, replace = TRUE)

##  [1] "AB" "B"  "A"  "A"  "O"  "A"  "A"  "O"  "O"  "O"  "O"  "O"  "O"  "O"  "O"  "O"  "O"  "A"  "O" 
## [20] "B"  "O"  "O"  "A"  "O"  "A"  "O"  "O"  "A"  "B"  "O"

Observe that a large sample reproduces the original probabilities with reasonable accuracy:

sim_data <- sample(
  x = bloodtypes, size = 10000,
  prob = bloodprobs, replace = TRUE
)
table(sim_data)

## sim_data
##    A   AB    B    O 
## 4006  364 1081 4549

table(sim_data) / 10000

## sim_data
##      A     AB      B      O 
## 0.4006 0.0364 0.1081 0.4549

The goal of simulation is usually to estimate the probability of an event. We will do this by creating a logical vector, that is a vector whose values are TRUE or FALSE. We simulate using a three-step process:

Simulate the experiment many times to produce a vector of outcomes.
Test if the outcomes are in the event to produce a logical vector we will call event.
Compute the mean of the vector event to compute the probability estimate.

Steps 1 and 2 can often be interesting problems, and their solutions can require creativity and expertise. Step 3 relies on the fact that R converts TRUE to 1 and FALSE to 0 when taking the mean of a vector. If we take the average of a vector of TRUE/FALSE values, we get the number of TRUE divided by the size of the vector, which is exactly the proportion of times that the event occurred. The theoretical justification for this procedure is given by the Law of Large Numbers.

Duplicate the work in Example 6.6 using the probabilities established for a rolling a pig. Use the probabilities given in Example 6.2.

Try it for yourself and then you can watch it be done in the video below.

Example 6.7 (Looking for Specific Dice Rolls) Suppose that two six-sided dice are rolled and the numbers appearing on the dice are added. We want to estimate the probability that the sum of the dice is 6 and that one of the dice is a 2.

For Step 1, we simulate this experiment by performing 10,000 rolls of each die with sample and then adding the two dice:

die1 <- sample(x = 1:6 , size = 10000 , replace = TRUE)
die2 <- sample(x = 1:6 , size = 10000 , replace = TRUE)
sumDice <- die1 + die2

Let’s take a look at the simulated data:

head(die1)

## [1] 4 4 6 5 4 1

head(die2)

## [1] 2 4 6 2 1 4

head(sumDice)

## [1]  6  8 12  7  5  5

Our first roll resulted in a 4 and a 2. Our second roll resulted in a 4 and a 4 and so on. Of the first six rolls, we get that only the first roll was good because it satisfies both of the conditions of the event we are interested in.

We are now ready for Step 2, to do this we let $E$ be the event “the sum of the dice is 6,” and $F$ be the event “at least one of the dice is a 2.” We define these events from our simulated data:

eventE <- sumDice == 6
head(eventE)

## [1]  TRUE FALSE FALSE FALSE FALSE FALSE

eventF <- die1 == 2 | die2 == 2
head(eventF)

## [1]  TRUE FALSE FALSE  TRUE FALSE FALSE

Here, $F$ is interpreted as “die 1 is a two or die 2 is a two” and uses R’s “or” operator |.

To see which rolls satisfy both $E$ and $F$ both being true, we use R’s “and” operator & and look at the first few results:

event <- eventE & eventF
head(event)

## [1]  TRUE FALSE FALSE FALSE FALSE FALSE

As we saw before, of the first six rolls, only the first one satisfies the conditions we want so it returns TRUE while the remaining shown rolls return a FALSE. We now have a vector called event which contains only the values TRUE and FALSE. That is, we have created a logical vector.

We are finally ready for Step 3. Using mean we find out what percentage of the time our events occurred in the simulation, which estimates the correct probabilities:

mean(event)

## [1] 0.0541

Thus, we have estimated that there is a $5.4\%$ chance that if you roll two dice, you will get a sum of 6 with one of the dice being a 2.

[Note: It is not necessary to store the individual logical vectors in event variables (eventE and eventF). Below is another line of code which gives the same result.]

mean((sumDice == 6) & (die1 == 2 | die2 == 2))

## [1] 0.0541

6.3.2 Using `replicate` to Repeat Experiments

The size argument of sample allowed us to perform many repetitions of an experiment. For more complicated probability experiments, we use the R function replicate(), which can take a single R expression and repeat it many times.

The function replicate is an example of an implicit loop in R. Suppose that expr is one or more R commands, the last of which returns a single value. The call

replicate(n , expr)

repeats the expression stored in expr a series of n times and stores the resulting values as a vector.

Example 6.8 (Rolling Seven Dice) Estimate the probability that the sum of seven dice is larger than 30.

To simulate this event once, we can use sample to roll seven dice, sum to add them, and then test for the event “the sum is larger than 30”:

dice <- sample(x = 1:6 , size = 7 , replace = TRUE) # roll seven dice
dice #look at the resulting 7 dice

## [1] 4 4 6 5 4 1 5

sum(dice) #calculate the sum

## [1] 29

sum(dice) > 30 # test if the event occurred

## [1] FALSE

If we click through the above code again, we will get new results like those below below:

## [1] 2 3 1 6 3 1 5

## [1] 21

## [1] FALSE

The result of this single simulation was FALSE.

We can now use replicate to repeat the experiment many times:

replicate(20, {
  dice <- sample(x = 1:6 , size = 7 , replace = TRUE) # roll seven dice
  dice #look at the resulting 7 dice
  sum(dice) #calculate the sum
  sum(dice) > 30 # test if the event occurred
})

##  [1]  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
## [17] FALSE FALSE FALSE FALSE

The curly braces { and } are required to replicate more than one R command. When you put multiple commands inside {} you are creating a code block. A code block acts like a single statement, and only the result of the last command is saved in the vector via replicate. As our last command is a logical statement, the result of this replicate is a logical vector like we used earlier.

Using multiple lines for a code block is not required but highly recommended for readability and debugging your code. It is also legal to put the entire code block on a single line and separate each command in the block with a semicolon.

Finally, we want to compute the probability of the event. We replicate 10,000 times for a reasonably accurate estimate:

event <- replicate(10000, {
  dice <- sample(x = 1:6 , size = 7 , replace = TRUE) # roll seven dice
  dice #look at the resulting 7 dice
  sum(dice) #calculate the sum
  sum(dice) > 30 # test if the event occurred
})
mean(event)

## [1] 0.0945

Since replicate only returns the last command of a block of code, the above replicate will return a logical vector and the middle “debug” lines can be omitted as shown below.

event <- replicate(10000, {
  dice <- sample(x = 1:6 , size = 7 , replace = TRUE) # roll seven dice
  sum(dice) > 30 # test if the event occurred
})
mean(event)

## [1] 0.0946

When rolling seven dice, there is about a $9.46\%$ probability the sum will be larger than 30. How accurate is our estimate? It is often a good idea to repeat a simulation a couple of times to get an idea about how much variance there is in the results. Running the code a few more times gave answers 0.0947, 0.091, 0.0965, and 0.0867. It seems safe to report the answer as roughly 9%.

The more replications you perform with replicate, the more accurate you can expect your simulation to be. On the other hand, replications can be slow. For events which are not rare, 10,000 trials runs quickly and gives an answer accurate to about two decimal places.

Remark. For complicated simulations, we strongly recommend that you follow the workflow as presented above; namely,

1. Write repeatable code that performs the experiment a single time.

2. Replicate the experiment a small number of times and check the results.

replicate(100 , { EXPERIMENT GOES HERE })

3. Replicate the experiment a large number of times and store the result.

event <- replicate(10000 , { EXPERIMENT GOES HERE })

4. Finally, estimate the probability using mean.

mean(event)

It is much easier to trouble-shoot your code this way, as you can test each line of your simulation separately.

Three dice are thrown. Estimate the probability that the largest value is a four.

Example 6.9 (Do Two Dice Sum to Six) The purpose of this example is to investigate the rate at which the proportion of successes converges to the true probability in a specific setting. To do so, we need to choose an experiment and an event $E$ for which we know the probability.

Suppose two dice are rolled. Let $E$ denote the event that the sum of the dice is six. It can be found with basic counting techniques that the probability is $\frac{5}{36} \approx 0.138888$.

The single line we need to replicate is

sum( sample( x = 1:6 , size = 2 , replace = TRUE ) ) == 6

because this code samples two values from 1 to 6 (with replacement), adds the values, and tests whether the sum is 6. You can run this single line repeatedly in R to see that it usually gives FALSE but occasionally gives TRUE.

We can now replicate this line and take the mean of the result. If we use 10 trials to estimate the probability, then the closest we can get is 0.1 because the result will be a fraction of form $k/10$ where $k$ is $0,1,2, \ldots, 9$ or $10$. We recommend running the code below several times to see that we sometimes get 0.1, but many times also get 0, 0.2, or 0.3.

mean(replicate(10 , {
  sum( sample( x = 1:6 , size = 2 , replace = TRUE ) ) == 6
}))

## [1] 0.3

On the other hand, when we use 200 trials, we are unlikely to be wrong in the first significant digit.

mean(replicate(200 , {
  sum( sample( x = 1:6 , size = 2 , replace = TRUE ) ) == 6
}))

## [1] 0.14

If we increase to 10,000 trials, we are even closer on average.

mean(replicate(10000 , {
  sum( sample( x = 1:6 , size = 2 , replace = TRUE ) ) == 6
}))

## [1] 0.1379

In Figure 6.5, we estimated the probability of $E$ for simulations ranging from 10 trials to 10,000 trials and then plotted the results.

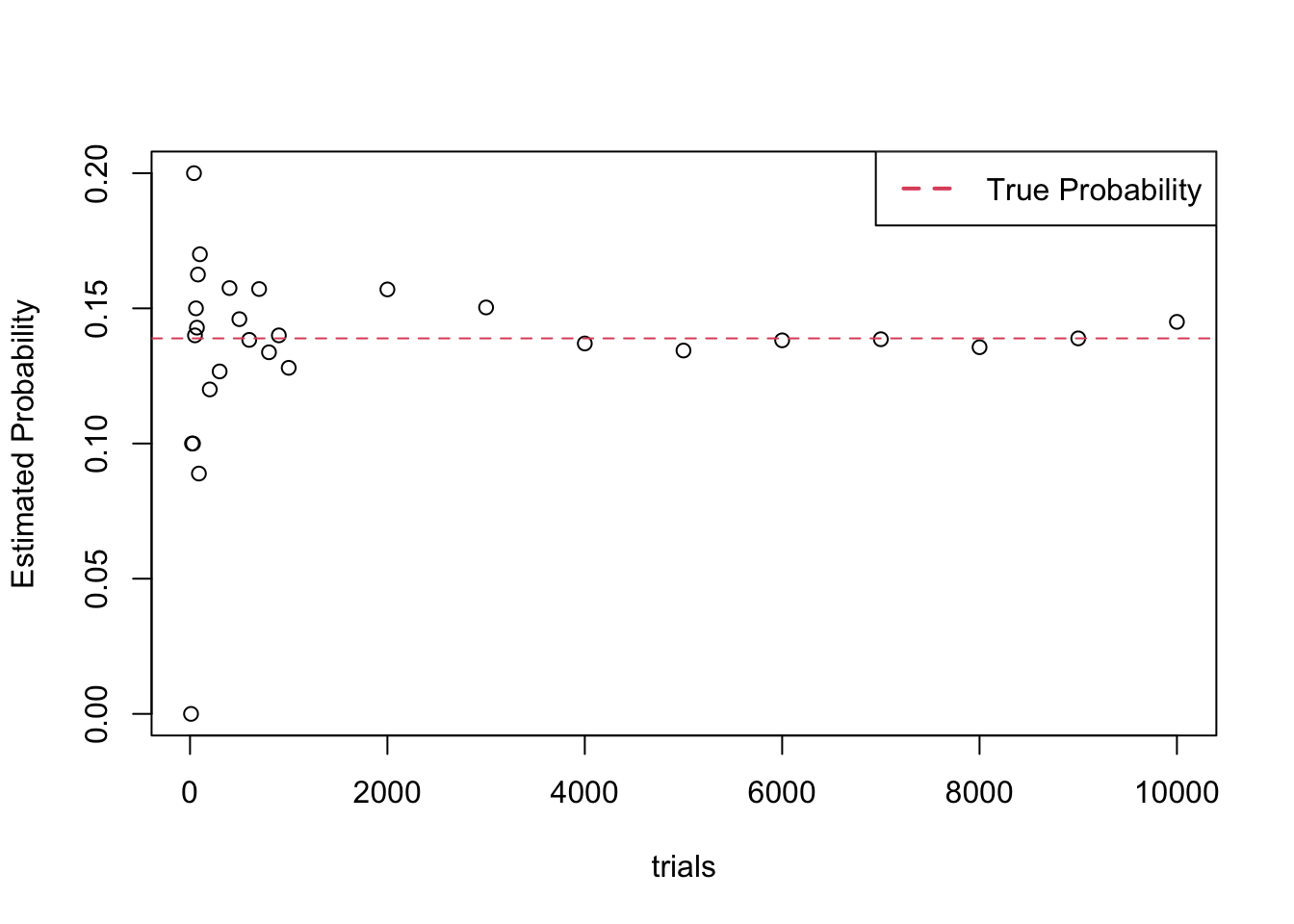
Illustration of the Law of Large Numbers. Probability estimates from simulation converge to the true probability as the number of trials increases.

Figure 6.5: Illustration of the Law of Large Numbers. Probability estimates from simulation converge to the true probability as the number of trials increases.

Remark. The downside to using more trials is that it takes more time to do the simulation, which can become very important if each trial itself takes a considerable amount of time. As a general rule of thumb, we have found that using 10,000 trials is a good compromise between speed and accuracy.

Example 6.10 (Flipping A Coin Example) A fair coin is repeatedly tossed. Estimate the probability that you observe heads for the third time on the 10th toss.

In this example, an outcome of the experiment is ten tosses of the coin. The event “you observe heads for the third time on the 10th toss” is complicated, and most of the work involves testing whether that event occurred.

Step 1: As before, we build this up in stages. Begin by simulating an outcome, a sample of ten tosses of a coin:

coinToss <- sample( x = c("H" , "T") , size = 10 , replace = TRUE )
coinToss

##  [1] "T" "T" "T" "H" "H" "H" "H" "H" "H" "H"

In order for the event to occur, we need for there to be exactly three heads, so we count the number of heads and check whether it is equal to three:

sum( coinToss == "H" )

## [1] 7

Recall that R treats TRUE as 1 when making certain calculations, so sum simply counts the number of times the value is "H".

sum( coinToss == "H" ) == 3

## [1] FALSE

Next, we also need to make sure that we had only two heads in the first nine tosses. So, we look only at the first nine tosses:

coinToss[1:9]

## [1] "T" "T" "T" "H" "H" "H" "H" "H" "H"

and add up the heads observed in the first nine tosses:

sum( coinToss[1:9] == "H" ) == 2

## [1] FALSE

Note that both of those have to be true in order for the event to occur:

sum( coinToss == "H" ) == 3 & sum( coinToss[1:9] == "H" ) == 2

## [1] FALSE

It is worth noting that our experiment is actually a combination of the lines above. If you run the following block of code, you should get one trial of our experiment.

coinToss <- sample( x = c("H" , "T") , size = 10 , replace = TRUE )
coinToss
sum( coinToss == "H" ) == 3 & sum( coinToss[1:9] == "H" ) == 2

Step 2: We now run our experiment a few trials and we observe that sometimes the event occurs and sometimes it does not:

replicate(20 , {
  coinToss <- sample( x = c("H" , "T") , size = 10 , replace = TRUE )
  coinToss
  (sum( coinToss == "H" ) == 3) & (sum( coinToss[1:9] == "H" ) == 2)
})

##  [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [17] FALSE FALSE FALSE FALSE

Step 3: We now run the full simulation:

event <- replicate(10000 , {
  coinToss <- sample( x = c("H" , "T") , size = 10 , replace = TRUE )
  coinToss
  (sum( coinToss == "H" ) == 3) & (sum( coinToss[1:9] == "H" ) == 2)
})

Step 4: We can now estimate the probability using mean.

mean(event)

## [1] 0.0362

The probability of observing heads for the third time on the 10th toss is about $3.5\%$.

Remark. In the example above, the test that there were three total heads but only two on the first nine tosses is not the only way to approach this problem. Here are two other tests that give the same result by looking at the tenth coin toss:

sum( coinToss == "H" ) == 3 & coinToss[10] == "H"

## [1] FALSE

sum( coinToss[1:9] == "H" ) == 2 & coinToss[10] == "H"

## [1] FALSE

This illustrates an important concept. There is NOT just one way to do things in R. Different people will often come up with different solutions which are equally valid. So, do not be discouraged if your efforts do not match either your group members, your teacher, or even this book.

Example 6.11 (The Birthday Problem) Estimate the probability that out of 25 randomly selected people, at least two will have the same birthday. Assume that all birthdays are equally likely, except that none are leap-day babies.

Step 1: An outcome of this experiment is 25 randomly selected birthdays, and the event is that at least two birthdays are the same. We can simulate the experiment with sample:

birthdays <- sample( x = 1:365 , size = 25 , replace = TRUE )
birthdays

##  [1] 228  35 340 114 295 207  48 352 224 278 252 245 233  23  45 242 246  75 203 116 153  75 281  68
## [25] 279

Next, we test for the event. In order to do this, we need to be able to find any duplicates in a vector. R has many, many functions that can be used with vectors. For most things that you want to do, there will be an R function that does it. In this case it is anyDuplicated(), which returns the location of the first duplicate if there are any, and zero otherwise. The important thing to learn here isn’t necessarily this particular function, but rather the fact that most tasks are possible via some built-in functionality.

anyDuplicated( birthdays )

## [1] 22

It happens that our sample did have two of the same birthday. At location 22 of the birthday vector, the number 75 appears. That same number showed up earlier in location 18. The event occurred in this example, and we can test for it by checking that the result of anyDuplicated is larger than 0. Putting it all together we get a block of code that runs our experiment once and returns a logical result.

birthdays <- sample( x = 1:365 , size = 25 , replace = TRUE )
anyDuplicated( birthdays )
anyDuplicated( birthdays ) > 0

Step 2: Now that we think that we have repeatable code, we test it using a small, 100, number of trials.

replicate( n = 100 , {
  birthdays <- sample( x = 1:365 , size = 25 , replace = TRUE )
  anyDuplicated( birthdays )
  anyDuplicated( birthdays ) > 0
})

##   [1] FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE  TRUE  TRUE FALSE
##  [17] FALSE  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE FALSE
##  [33]  TRUE FALSE  TRUE  TRUE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE  TRUE  TRUE  TRUE FALSE  TRUE
##  [49] FALSE  TRUE  TRUE FALSE FALSE FALSE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE FALSE
##  [65]  TRUE FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE
##  [81]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE
##  [97]  TRUE  TRUE FALSE  TRUE

We see that we have a smattering of TRUEs and FALSEs, so we are confident to push to a full simulation.

Step 3: We now run the full simulation.

eventBirthday <- replicate( n = 10000 , {
  birthdays <- sample( x = 1:365 , size = 25 , replace = TRUE )
  anyDuplicated( birthdays ) > 0
})

Step 4: We now simply use mean to finish our work.

mean( eventBirthday )

## [1] 0.5726

The probability of this event is approximately 0.57. Interestingly, we see that it is actually quite likely that a group of 25 people will contain two with the same birthday.

We skip showing the step of trying our experiment over a small number of trials in the example below. However, as you work through your own simulations, we strongly encourage you to not omit this step until you have enough experience. Even with experience, sticking to the four steps is a great way to troubleshoot code that isn’t working as you expect.

Example 6.12 (First Look at M&Ms) According to Rick Wicklin⁴⁸, the proportion of M&M’s of various colors produced in the New Jersey M&M factory are as shown in the table below.

M&M Candies, Photo by [Evan Amos](https://commons.wikimedia.org/wiki/File:Plain-M&Ms-Pile.jpg)

Figure 6.6: M&M Candies, Photo by Evan Amos

\[\begin{array}{|l|c|} \hline \text{Color} & \text{Percentage}\\ \hline \text{Blue} & 25.0\\ \text{Orange} & 25.0\\ \text{Green} & 12.5\\ \text{Yellow} & 12.5\\ \text{Red} & 12.5\\ \text{Brown} & 12.5\\ \hline \end{array}\]

If you buy a bag from the New Jersey factory that contains 35 M&M’s, what is the probability that it will contain exactly 9 Blue and 5 Red M&M’s?

To do this, we can use the prob argument in the sample function, as follows.

mm.colors <- c( "Blue", "Orange", "Green", "Yellow", "Red", "Brown" )
mm.probs <- c( 25, 25, 12.5, 12.5, 12.5, 12.5 )
bag <- sample(
  x = mm.colors,
  size = 35,
  replace = TRUE,
  prob = mm.probs
)
sum( bag == "Blue" ) # counts the number of Blue M&M's

## [1] 6

event <- replicate(10000 , {
  bag <- sample(
    x = mm.colors,
    size = 35,
    replace = TRUE,
    prob = mm.probs
  )
  sum( bag == "Blue" ) == 9 & sum( bag == "Red" ) == 5
})
mean( event )

## [1] 0.0282

6.4 Continuous Probabilities

Thus far, all of the random variables that we have worked with have been Discrete Random Variables. We now move on to where the random variable can take on values across a continuous region of the real line.

Definition 6.7 If a random variable can take on any value inside a continuous interval $(a,b)$ inside the real numbers, then we call it a Continuous Random Variable. We require that

\[P( X= x_0 ) = 0\] for any value $x_0\in (a,b)$. The fact that the probability of equaling any given value is zero is what we call the Continuous Variable Axiom.

Remark. The restriction that $P(X = x_0) = 0$ will ensure that the Distribution Function we define in Section 6.5.2 will be continuous as long as $X$ is a continuous random variable.

According to Snickers.com, as of early 2025, the weight of a Snickers bar in the United States is 1.86 ounces. However, it is not possible to produce physical bars that are exactly 1.86 ounces nor is it possible to produce bars which have identical weights if we measure to a high enough level of precision. To understand the distribution of weights of Snickers bars, we will use the vector Snickers which contains the weight of 100 Snickers bars.

The reader can see Section 6.7.2 to get more information about this dataset.

Snickers <- c( 
51.1, 53.8, 51.1, 53.8, 51.9, 52.5, 53.2, 53.8, 52.4, 54.0, 
53.5, 54.4, 51.1, 52.4, 50.8, 52.1, 51.9, 51.2, 52.7, 53.3, 
52.1, 54.1, 52.7, 54.1, 51.9, 53.7, 52.2, 53.7, 54.2, 52.2, 
52.5, 54.5, 53.0, 51.9, 54.4, 54.7, 53.0, 53.8, 54.3, 53.3, 
52.4, 51.2, 53.5, 52.4, 52.3, 55.2, 51.2, 54.3, 53.3, 51.9, 
51.3, 53.8, 53.3, 52.0, 50.3, 51.8, 51.1, 52.6, 52.5, 53.9, 
53.1, 53.9, 52.9, 52.2, 50.5, 52.5, 50.3, 52.2, 52.2, 51.7, 
52.0, 52.5, 53.1, 53.8, 54.0, 53.4, 52.3, 50.9, 53.9, 53.4, 
53.4, 52.5, 53.6, 53.0, 56.2, 54.2, 52.5, 52.4, 53.3, 52.9, 
51.8, 50.9, 52.3, 54.0, 51.2, 53.6, 51.1, 50.3, 53.2, 52.6 
)/28.35

We can look at the first few values of Snickers using head.

head( Snickers )

## [1] 1.802469 1.897707 1.802469 1.897707 1.830688 1.851852

We can also run summary on Snickers to get a quick look at some of the numerical summaries of our data.

summary( Snickers )

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   1.774   1.833   1.855   1.860   1.894   1.982

We see that our data gives a mean right at 1.86 ounces.

Construct a boxplot of Snickers and discuss what type of skew you see in the data. Does the skew seem to favor the consumer or the manufacturer?

We continue on with our analysis of Snickers by looking at a histogram.

SnickersHist <- hist( Snickers )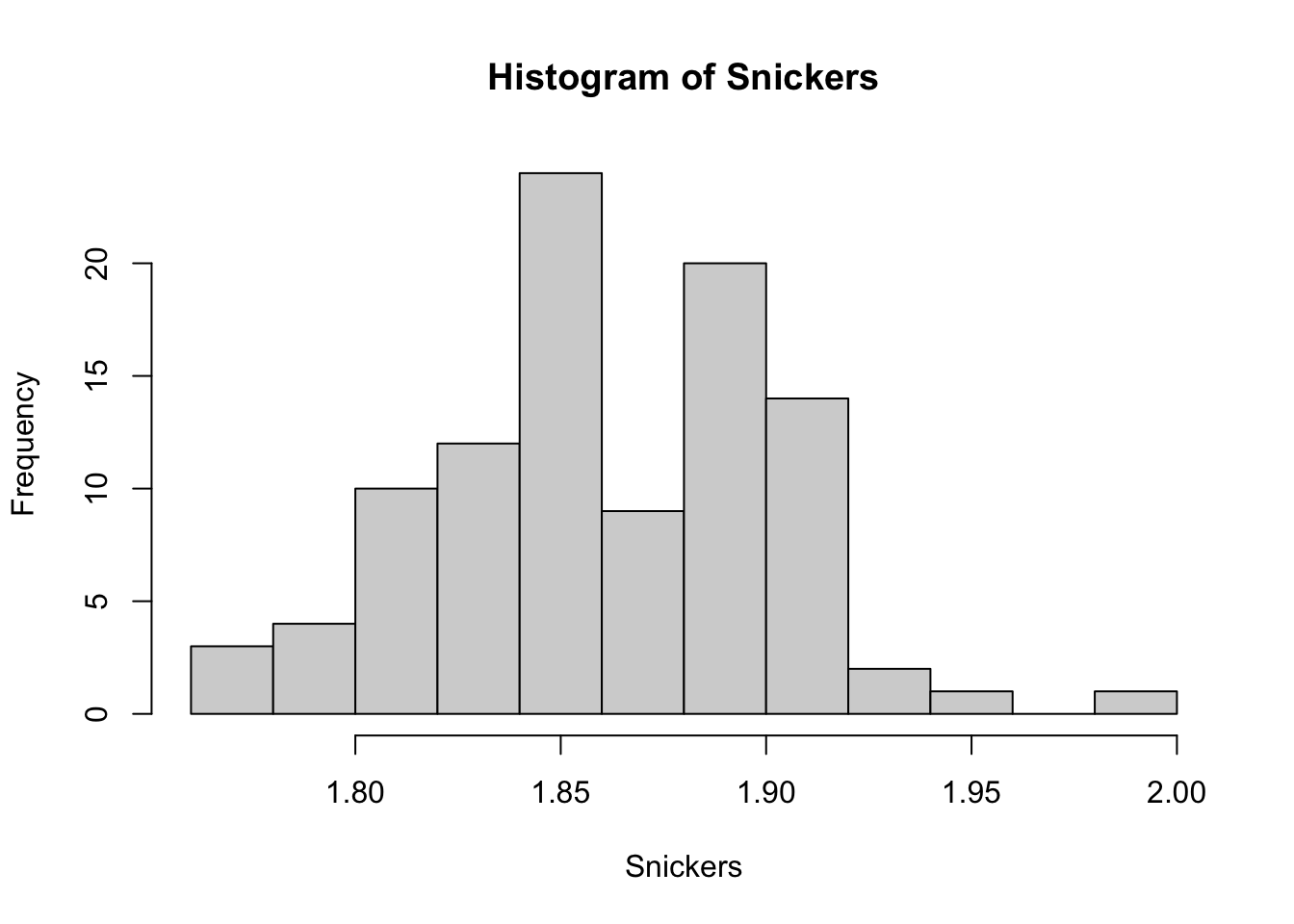

Figure 6.7: Frequency Histogram of Snickers Bar Weights (oz)

Remark. Here we saved hist( Snickers ) as SnickersHist which will allow us to extract more information from Snickers than just the plot we see above. By default, hist returns a list of six different variables. The curious reader can examine this in more detail by looking at ?hist and scrolling down to the Value section of the help file.

For discrete data, the area of the bars in a relative frequency histogram was equivalent to the proportion. Let’s pull out the frequencies of each bin to find the area of the boxes in our histogram

SnickersHist$counts

##  [1]  3  4 10 12 24  9 20 14  2  1  0  1

To get the areas of the boxes, we need to know precisely how wide the bins are. We can find this by looking at the boundary of the bins using the breaks column of SnickersHist.

SnickersHist$breaks

##  [1] 1.76 1.78 1.80 1.82 1.84 1.86 1.88 1.90 1.92 1.94 1.96 1.98 2.00

Thus, the areas of the boxes can be found by multiplying the frequencies, which is contained in SnickersHist$counts, by the width of each bin which is 0.02.

SnickersHist$counts*0.02

##  [1] 0.06 0.08 0.20 0.24 0.48 0.18 0.40 0.28 0.04 0.02 0.00 0.02

To compare our histogram to the area idea we developed from discrete bar plots, we find the sum of the areas of the rectangles.

sum( SnickersHist$counts*0.02 )

## [1] 2

To make the setup match what we had with the pigs in Section 6.1 we would want to not use the counts, but the counts divided by exactly 2 so that this sum would be 1 so that we can be consistent with Definition 6.2.

If we set freq = FALSE in hist, this is exactly what the values on the vertical axis are!

hist( Snickers, freq = FALSE)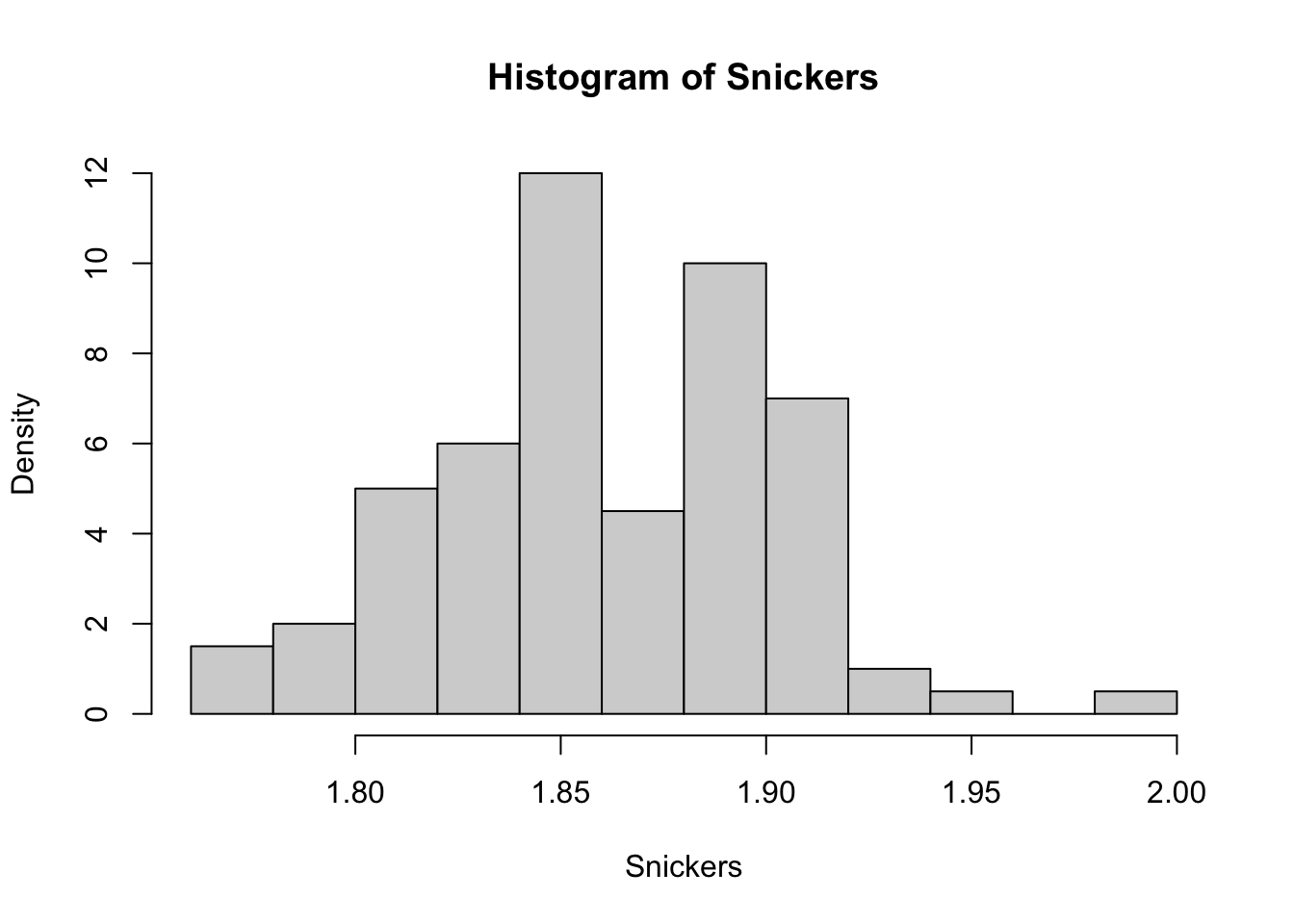

Figure 6.8: Density Histogram of Snickers Bar Weights (oz)

Thus what R is labeling as Density in Figure 6.8 is the height of the box needed so that the proportion of values in the bin is equal to the area of the box. This leads us to our definition of Density in the case of a histogram.

Definition 6.8 The Density of a histogram bin is the height such that the area of the rectangle is equal to the proportion of values that fall within that bin.

Remark. The careful reader will likely wonder about using histograms for discrete values in Section 6.1 instead of bar plots when the data was numeric. We will require that discrete random variables take on integer values so that the bins will have width of 1 like we setup in Section 3.3.2. This will ensure that the height of each rectangle is equal to its area so that that density and proportion are interchangeable.

We can also find the densities of a histogram directly using the density column of a saved histogram like below.

SnickersHist$density

##  [1]  1.5  2.0  5.0  6.0 12.0  4.5 10.0  7.0  1.0  0.5  0.0  0.5

6.5 Probability Functions

As we get towards the end of this chapter, we want to establish the structure we will use with random variables. These functions will allow us to use random variables to analyze and understand probability questions as well as lead us towards being able to make inferences about a population based on the statistics we have from a sample.

6.5.1 Density Function

In Section 6.4, we defined density in terms of a bin in a histogram. It is the goal of this section to define it for each value that a random variable can take. If we have a discrete random variable, the remark at the end of Section 6.4 means we can simply define the density of a discrete random variable to be the density we defined for the bin of width 1 as we setup in Section 3.3.2.

This leads us to the idea of assigning the density of a bin to the midpoint of the bin, but this only allows us to define it for a number of values of the data equal to the number of bins in the histogram. Thus, to define density for more values, we need to have histograms with more bins, a lot more bins.

To be able to get meaningful information from a histogram with a lot of bins, we need a lot more bars than one hundred. We will look at the histogram of a sample of one hundred thousand Snickers bars.⁴⁹ We start with an artificially small number of bins.

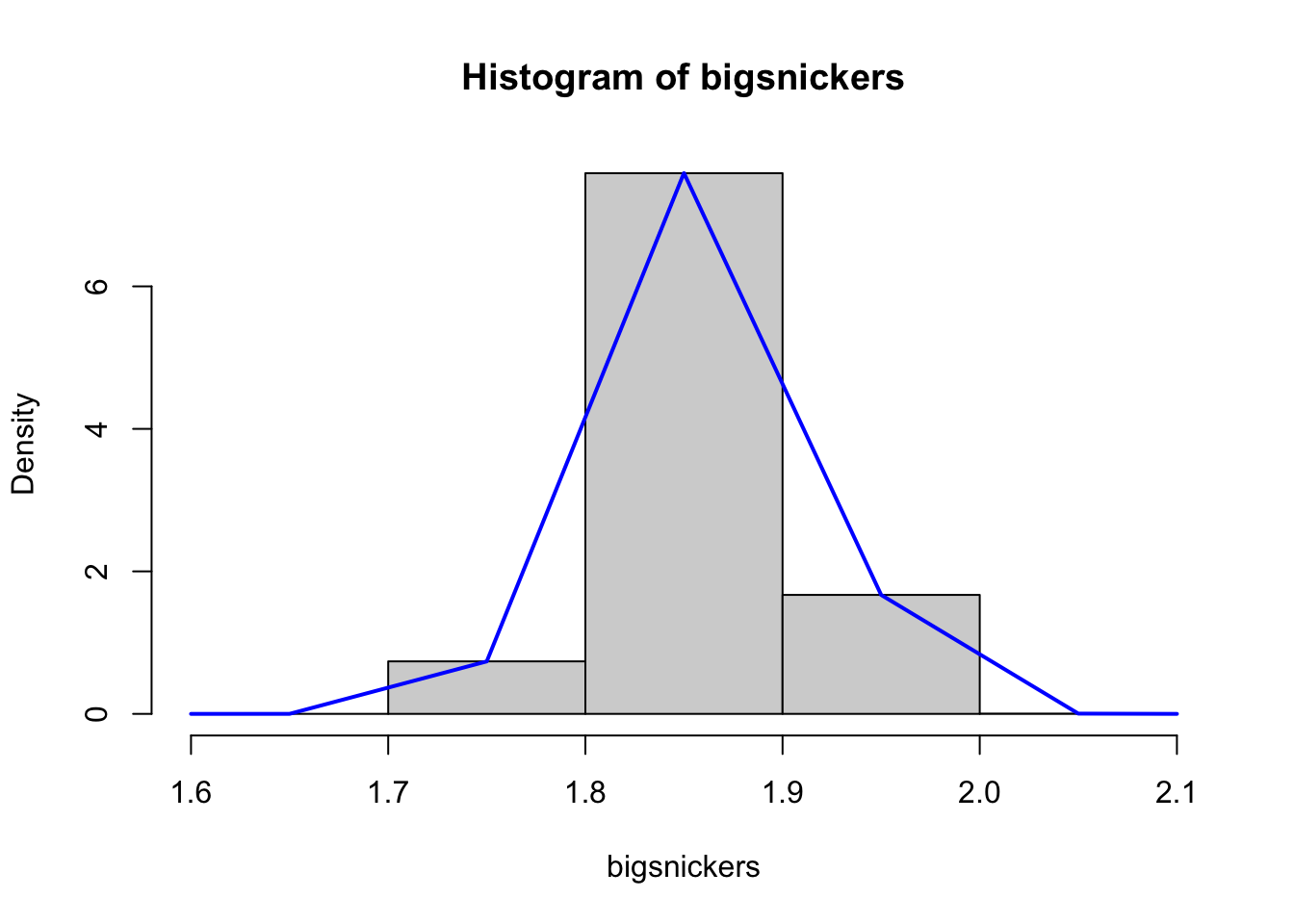
Figure 6.9: Density Histograms of Snickers Bar Weights with 5 Bins

The blue curve⁵⁰ on top of the histogram is created by connecting the top of each rectangle at the midpoint of each bin. This means that the blue curve can be taken as a function which defines the density for all of the values in the range of the histogram. However, as we mentioned, the number of bins in Figure 6.9 was artificially set to be low, only 5 in this case.

If we increase the number of bins to only 8, we get the following plot.

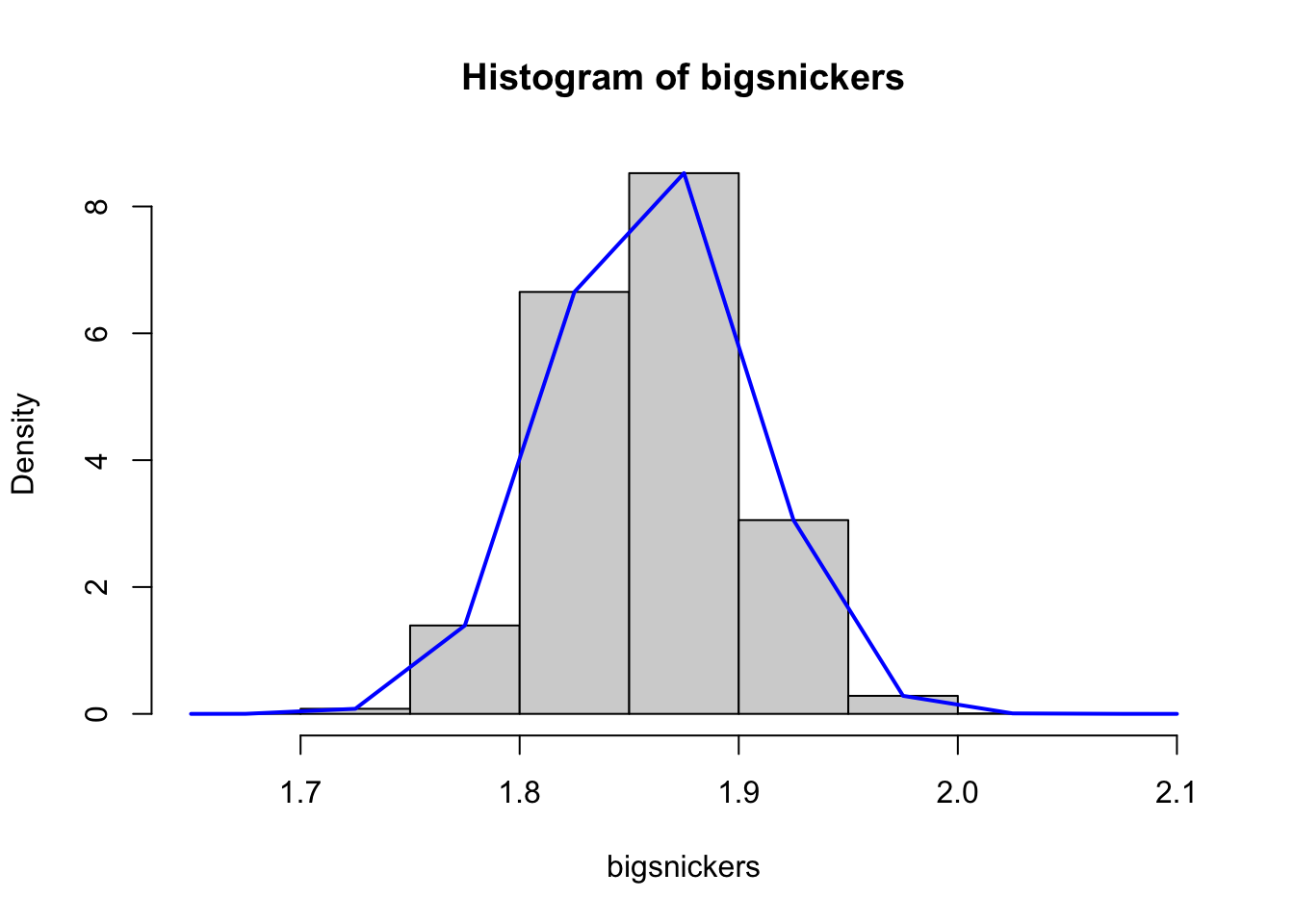
Figure 6.10: Density Histograms of Snickers Bar Weights with 8 Bins

If we again view the blue curve as the density function, we see that we are getting more detail in the curve and that it would give more “correct values” (i.e. that match the histogram) since there are more bins.

Naturally, we can increase the number of bins even further, this time to 18.

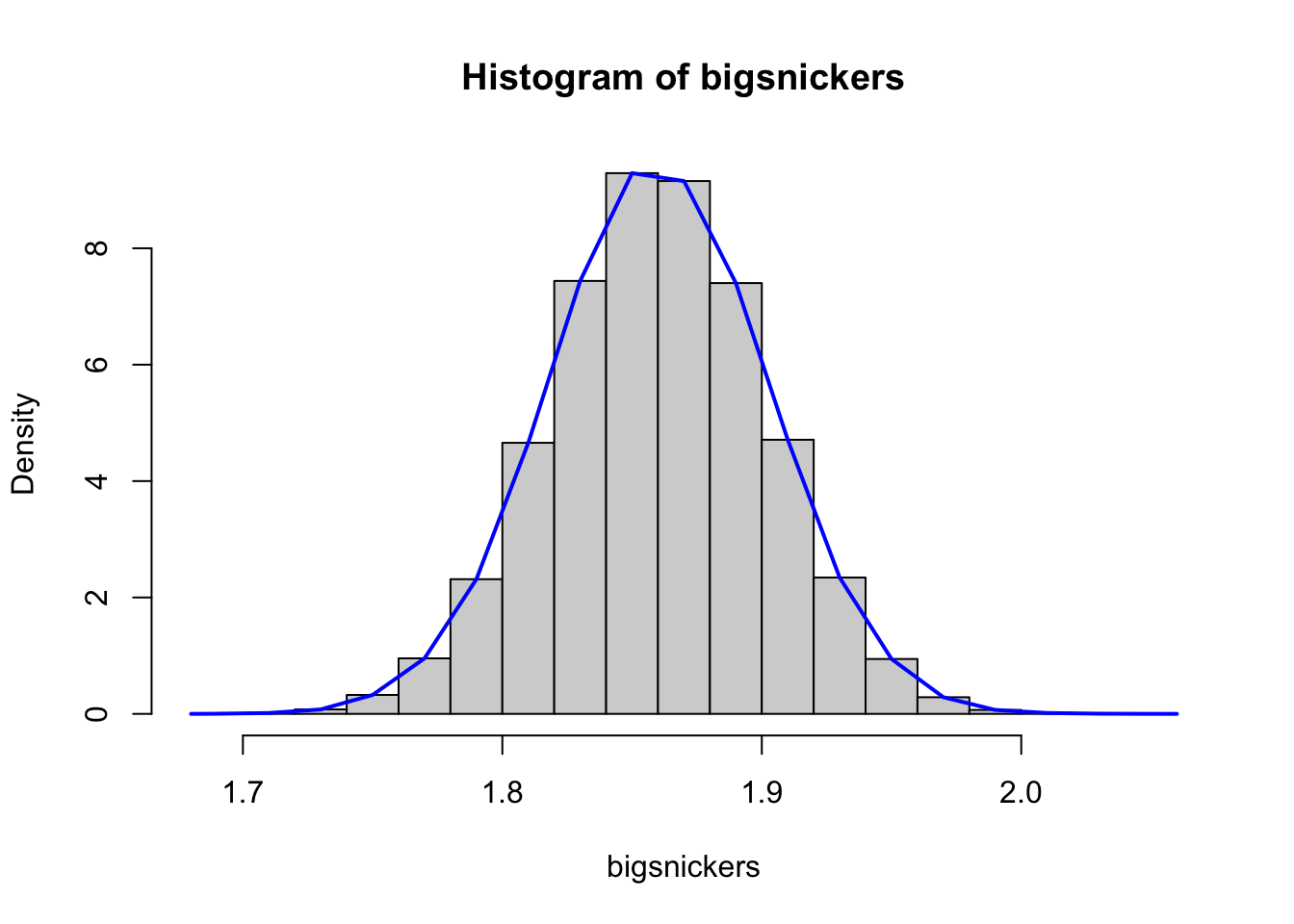
Figure 6.11: Density Histograms of Snickers Bar Weights with 18 Bins

The blue curve in Figure 6.11 is starting to actually look a true “curve” in the more basic sense of the word.

As we increase the number of bins in a histogram, the density “polygon” we have been creating appears to be approaching a smooth curve.

Cranking up the number of bins to 68 gives the following plot.

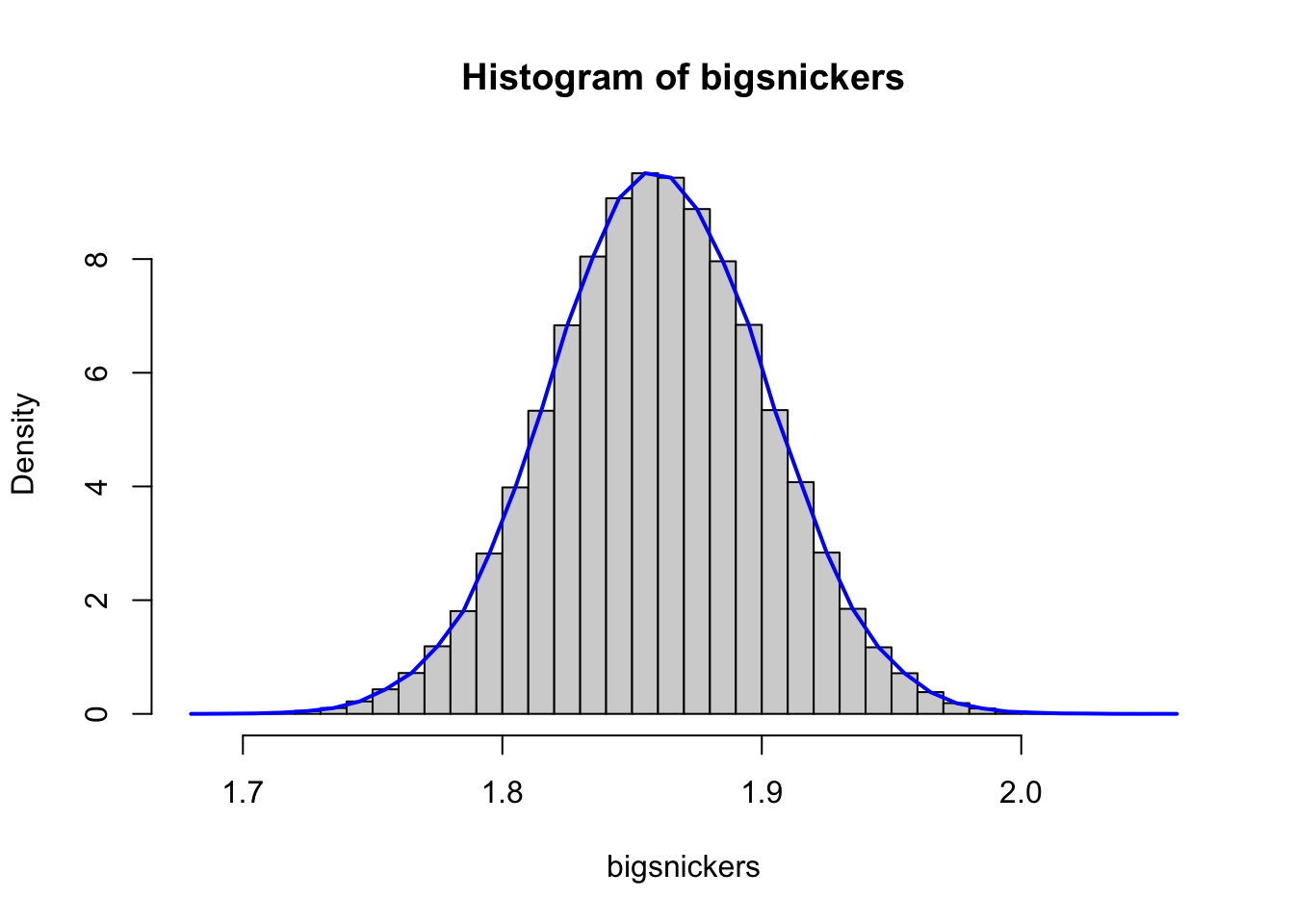
Figure 6.12: Density Histograms of Snickers Bar Weights with 68 Bins

Figure 6.12 looks like a smooth curve at first glance, but if one looks very closely at it, especially near the middle of the values, it can be seen to still be made up of straight line segments.

This concept can continue to get a function which is “correct” at as many points as we wish as long as we have enough data values in our histogram. Imagining the possibility of making a histogram of an infinite number of Snickers bars using an infinite number of bins would yield a curve that looks like the following.

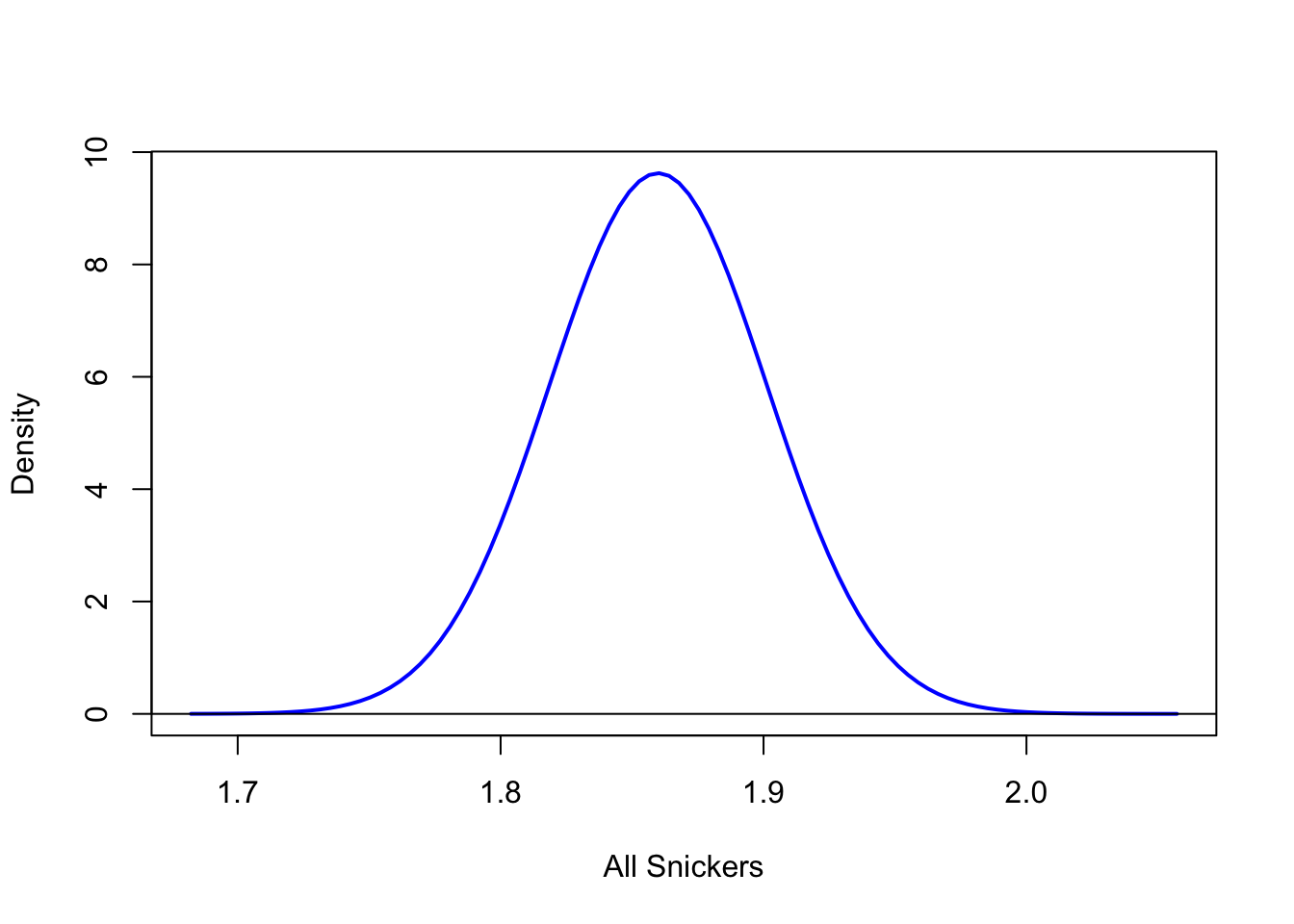
Figure 6.13: Density Function of Snickers Bars

Being that each histogram in Figures 6.9 to 6.12 was defined to have a total area of 1 when we add the area of the rectangles, we get that the area bound by the blue curve and the $x$-axis is 1 as well. This leads us to the definition of a Density Function.

Definition 6.9 Given a random variable that can take on any value on a continuous interval of the real line, we define the Density Function of a Continuous Random Variable to be the function that results from using the technique outlined above between Figures 6.9 to 6.12 and resulting in a graph like seen in Figure 6.13. If this function is called $\text{ddist}$, then we demand it satisfy the following:

$\text{ddist}$ is a continuous function
$\text{ddist}(x) \geq 0$ for all values of $x$.
The area under the graph of $\text{ddist}(x)$ is equal to 1⁵¹.
$P( a < X \leq b)$ is the area under the curve, $y = \text{ddist}(x)$, between $x=a$ and $x=b$.

To understand the density of a continuous random variable, we can use the following Desmos exploration.

[Note: You should be able to dynamically interact with the above figure.]

If you change the values of $a$ and $b$ by dragging the points along the $x$-axis, we get a new probability of form $P(a < X\leq b)$.

For completeness, we will give a different definition of a Density Function for a discrete random variable.

Definition 6.10 Given a random variable that can take values within a subset of the integers, we define the Density Function of a Discrete Random Variable to be a function, $\text{ddist}$, that satisfies the following:

$P( X = x_0 ) = \text{ddist}( x_0 )$ for all integers $x_0$.
$\text{ddist}(x) \geq 0$ for all values of $x$.
$\sum \text{ddist}(x_i) = 1$ where the sum is taken over all integers, $x_i$.

Remark. Definition 6.10 does allow for $\text{ddist}$ to be defined for more values than just the integers so that we can view it as the “tops” of a histogram as seen in Section 3.3.2.

6.5.2 Distribution Function

The density function above makes it easy to define what we will call the Distribution Function.

Definition 6.11 Given a random variable, $X$, we define the Distribution Function of it to be a function $\text{pdist}$ that satisfies

\[\text{pdist}(q )= P(X \leq q)\] for any real number $q$

It is important to note that we will not show any graphs of distribution functions or the quantile functions we will shortly define in Section 6.5.3. All of the graphs shown in this book are the graphs of density functions. However, we will learn how to interpret the distribution and quantile functions based off of density graphs.⁵²

We can explore a generic distribution function using the Desmos exploration below which you can interact with.

Feel free to play around with it and then watch the following video walking through it.

6.5.3 Quantile Function

Due to the exploration we just looked at, we can see that there is a one to one correspondence between the quantiles and the probabilities. This leads us to consider the inverse function of $\text{pdist}$.

Definition 6.12 Given a random variable, $X$, with a distribution function, $\text{pdist}$, we define the variable’s Quantile Function to be a function $\text{qdist}$ defined by

\[\text{qdist}( p ) = \text{pdist}^{-1} (p).\]

Remark. There can be some issues with this definition if there is any open interval where $\text{ddist}$ is constant 0 for a continuous random variable. There can also be some trickiness in defining the quantile function for discrete random variables as only discrete values of probabilities are actually possible. Fortunately, these issues will not cause us much concern and we can use the above as our definitions.

We can explore a generic quantile function using the Desmos exploration below which you can interact with.

Feel free to play around with it and then watch the following video walking through it.

6.5.4 Random Function

We saw in Section 6.3 that simulations can offer a great way to run probability experiments. If we want to run probability experiments that can be modeled by random variables, we need a function that can generate random values of the variable.

Definition 6.13 Given a random variable, $X$, with a density function, $\text{ddist}$, we define the variable’s Random Generation Function to be a function $\text{rdist}$ that generates values that $X$ takes on. A large number of values obtained from $\text{rdist}$ will yield a histogram which can be closely modeled by $\text{ddist}$.

The concept of a Random Generation Function is only necessary when running simulations. This concept may not be covered in some courses using this text.

6.6 Mind Your `p`’s and `q`’s⁵³

Keeping pdist and qdist straight can be difficult for new users. It can be helpful to think of the p being “probability”( or proportion) and q being “quantile”. So pdist is the function that has an output of p and qdist is the function that has an output of q.

q <- qdist( p )     #This code is not executable.
p <- pdist( q )     #This code is not executable.

Another way to think of it is that you put a p into qdist to get a q or inversely we put a q into pdist to get a p.

Review the explorations in Sections 6.5.2 and 6.5.3 if you are struggling to mind your ps and qs.

Exercises

Exercise 6.1 Suppose there are two boxes and each contain slips of papers numbered 1-8. You draw one number at random from each box.

Estimate the probability that the sum of the numbers is 8.
Estimate the probability that at least one of the numbers is a 2.

Exercise 6.2 Suppose the proportion of M&M’s by color is: \[ \begin{array}{cccccc} \text{Yellow} & \text{Red} & \text{Orange} & \text{Brown} & \text{Green} & \text{Blue}\\ 0.14 & 0.13 & 0.20 & 0.12 & 0.20 & 0.21 \end{array} \]

Estimate the probability that a random selection of four M&M’s will contain a blue one.
Estimate the probability that a random selection of six M&M’s will contain all six colors.
Suppose you buy a bag of M&M’s with 30 pieces in it. Estimate the probability of obtaining at least 9 Blue M&M’s and at least 6 Orange M&M’s in the bag.

Exercise 6.3 Blood types O, A, B, and AB have the following distribution in the United States in the table below. \[\begin{array}{lcccc} \text{Type} & A & AB & B & O\\ \text{Probability} & 0.40 & 0.04 & 0.11 & 0.45 \end{array}\] What is the probability that two randomly selected people have the same blood type?

Exercise 6.4 Use simulation to estimate the probability that a 10 is obtained when two dice are rolled.

Exercise 6.5 Estimate the probability that exactly 3 heads are obtained when 7 coins are tossed.

Exercise 6.6 Estimate the probability that the sum of five dice is between 15 and 20, inclusive.

Exercise 6.7 Suppose a die is tossed repeatedly, and the cumulative sum of all tosses seen is maintained. Estimate the probability that the cumulative sum ever is exactly 20. [Hint: the function cumsum() computes the cumulative sums of a vector.]

Exercise 6.8 Rolling different pairs of dice.

Simulate rolling two dice and adding their values. Perform 10,000 simulations and make a bar chart showing how many of each outcome occurred.
You can buy trick dice, which look (sort of) like normal dice. One die has numbers 5, 5, 5, 5, 5, 5. The other has numbers 2, 2, 2, 6, 6, 6. Simulate rolling the two trick dice and adding their values. Perform 10,000 simulations and make a bar chart showing how many of each outcome occurred.
Sicherman dice also look like normal dice, but have unusual numbers. One die has numbers 1, 2, 2, 3, 3, 4. The other has numbers 1, 3, 4, 5, 6, 8. Simulate rolling the two Sicherman dice and adding their values. Perform 10,000 simulations and make a bar chart showing how many of each outcome occurred. How does your answer compare to part a.?

Exercise 6.9 In a room of 200 people (including you), estimate the probability that at least one other person will be born on the same day as you.

Exercise 6.10 In a room of 100 people, estimate the probability that at least two people were not only born on the same day, but also during the same hour of the same day. (For example, both were born between 2pm and 3pm on March 27th, but possibly in different years.)

Exercise 6.11 Assume we roll a standard 6 sided die and a fair 12 sided die. Estimate the probability that the value on the 6 sided die is greater than that on the 12 sided one.

Exercise 6.12 Estimate the probability that the sum on two dice is greater than the sum on three dice.

Exercise 6.13 Watch the video below and show via simulation that the dice ranking shown in the video is correct.

Challenge Problems:

Exercise 6.14 Assuming that there are no leap-day babies and that all birthdays are equally likely, estimate the probability that at least three people have the same birthday in a group of 50 people. [Hint: try using table in RStudio.]

Exercise 6.15 Estimate the probability of having at least 6 successive Heads or Tails if you flipped a coin 100 times. What about 7 successive tosses of Heads or Tails? [Hint: Look up rle() in RStudio.]

Exercise 6.16 Refer to https://en.wikipedia.org/wiki/Craps#Pass_line and estimate the probability of winning a Pass line bet. [Warning: This will require more functions than given here.]

[Warning: The following problem(s) are even harder and will likely require a “loop” of some sort.]

Exercise 6.17 Deathrolling in World of Warcraft works as follows. Player 1 tosses a 1000-sided die. Say they get $x_1.$ Then player 2 tosses a die with $x_1$ sides on it. Say they get $x_2$. Player 1 tosses a die with $x_2$ sides on it. This pattern continues until a player rolls a 1. The player who loses is the player who rolls a 1 at which point the Deathroll ends.

Estimate the probability that a 1 will be rolled on the 4th roll in a Deathroll.
Estimate the average number of rolls when two people Deathroll.

6.7 Appendix

6.7.1 Cleaning the Pigs

Remark. Often the datasets you are asked to work with contain more information than you need or have information stored in a way that is not transparent. This section gives an example of “cleaning up” a dataset to be used.

The dataset we used in Section 6.1 came from a paper by Dr. John Kerr. The original data was contained in a .txt file which can be found here. This section will walk through the process of converting pig.data.txt to first a file called PigData.csv and then finally Pigs.csv.

The first step was done behind the scenes to convert pig.data.txt to PigData.csv which contains the same information but is now in the more readily usable .csv file type. We can then import the .csv into RStudio via the code below.

PigData <- read.csv( "https://statypus.org/files/PigData.csv" )

The two tasks we have left are to remove the 23 instances where the two pigs were touching which is accounted for as a value of 7. This is done with the following line creating a new data frame called PigTemp.

PigTemp <- PigData[ PigData$black != 7,]

This new data frame has 5,977 observations compared to PigData which had 6,000 observations. The final alteration we make to Dr. Kerr’s original data is to change the way the data is stored in the black and pink column like was discussed in the exercises in Chapter 1 about mtcars.

Using the dictionary we can get the relationship between the integers 1 through 6 as well as the name of the outcome of rolling a single pig. We can use the factor function⁵⁴ to change the integers 1 through 6 into the names we see below.

PigTemp$black <- factor( 
  PigTemp$black, levels = 1:6, 
  labels = c("Dot Up", "Dot Down", "Trotter", "Razorback", "Snouter", "Leaning Jowler") 
  )
PigTemp$pink <- factor( 
  PigTemp$pink, levels = 1:6, 
  labels = c("Dot Up", "Dot Down", "Trotter", "Razorback", "Snouter", "Leaning Jowler")
  )

We can see the difference between PigData and PigTemp most quickly by running str on each.

str( PigData )

## 'data.frame':    6000 obs. of  5 variables:
##  $ black : int  4 3 4 3 5 2 3 2 4 3 ...
##  $ pink  : int  1 4 4 1 1 4 2 5 1 4 ...
##  $ score : int  5 10 20 5 10 5 5 10 5 10 ...
##  $ height: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ start : int  0 0 0 0 0 0 0 0 0 0 ...

str( PigTemp )

## 'data.frame':    5977 obs. of  5 variables:
##  $ black : Factor w/ 6 levels "Dot Up","Dot Down",..: 4 3 4 3 5 2 3 2 4 3 ...
##  $ pink  : Factor w/ 6 levels "Dot Up","Dot Down",..: 1 4 4 1 1 4 2 5 1 4 ...
##  $ score : int  5 10 20 5 10 5 5 10 5 10 ...
##  $ height: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ start : int  0 0 0 0 0 0 0 0 0 0 ...

The obvious difference is that the variables black and pink in PigTemp are now saved as factors indicating in words the outcome of the roll rather than the integers we see in PigData. There is also 23 fewer observations in PigTemp which we removed because they had the value of 7 in both black and pink which indicated they were touching and thus weren’t of the valid types for a single pig roll.

To be able to share the file, we then write the data to a new .csv file which we call Pigs.csv and then this file was uploaded to Statypus.

write.csv( PigTemp, file="Pigs.csv", row.names = FALSE)

Remark. The astute reader will notice that the variable type of black and pink is Factor in this section but it was chr in Section 6.1. This is an artifact of using write.csv and then read.csv. For our purposes, this difference is inconsequential and we will not worry ourselves with trying to preserve the Factor variable type. However, if this a concern of yours, there are a few options such as using the csvy package. You can see Stack Overflow for more information.

6.7.2 Snickers Data

The Snickers data we used in Section 6.4 comes from data pulled from a post on Quora. The following code chunk is pulled directly from that discussion thread.

snickers <- c( 
51.1, 53.8, 51.1, 53.8, 51.9, 52.5, 53.2, 53.8, 52.4, 54.0, 
53.5, 54.4, 51.1, 52.4, 50.8, 52.1, 51.9, 51.2, 52.7, 53.3, 
52.1, 54.1, 52.7, 54.1, 51.9, 53.7, 52.2, 53.7, 54.2, 52.2, 
52.5, 54.5, 53.0, 51.9, 54.4, 54.7, 53.0, 53.8, 54.3, 53.3, 
52.4, 51.2, 53.5, 52.4, 52.3, 55.2, 51.2, 54.3, 53.3, 51.9, 
51.3, 53.8, 53.3, 52.0, 50.3, 51.8, 51.1, 52.6, 52.5, 53.9, 
53.1, 53.9, 52.9, 52.2, 50.5, 52.5, 50.3, 52.2, 52.2, 51.7, 
52.0, 52.5, 53.1, 53.8, 54.0, 53.4, 52.3, 50.9, 53.9, 53.4, 
53.4, 52.5, 53.6, 53.0, 56.2, 54.2, 52.5, 52.4, 53.3, 52.9, 
51.8, 50.9, 52.3, 54.0, 51.2, 53.6, 51.1, 50.3, 53.2, 52.6 
)

6.7.2.1 De-discretizing `snickers`

The vector snickers is the mass of the 100 Snickers bars as measured by David Sims on a triple beam balance. As mentioned at the start of Section 6.4, the variable of mass is a continuous variable, but in an essence we are viewing it as a discrete variable with units of a tenth of a gram. Discrete data will cause us issues with The Continuous Variable Axiom, Definition 6.7. For example, we can find the proportion of bars that match the first observed mass of 51.1 grams.

length( snickers[ snickers == 51.1 ] ) / length( snickers )

## [1] 0.05

This would translate to the statement that $P(X = 51.1 ) = 0.05$. To avoid this, we will convert the masses of the bars to their weight in ounces.⁵⁵ The conversion we will use is that 28.35 grams is equivalent to 1 ounce. So, we can convert the masses in snickers to weights in a new vector which we call Snickers.⁵⁶

Snickers <- snickers / 28.35

Looking at the values in Snickers shows that they do not appear discrete and will in practice guarantee that no value falls on the boundary of any bin of a histogram.

head( Snickers )

## [1] 1.802469 1.897707 1.802469 1.897707 1.830688 1.851852

These are the values we used in Section 6.4 to gain an understanding of the distinction between discrete and continuous data.

6.7.2.2 Generating 100,000 Snickers Bars

In Section 6.5.1, we looked at the distribution of one hundred thousand Snickers bars. As acknowledged in a footnote there, this data was simulated in R. This section talks about how this was done. The code below is how we generated the dataset we call bigsnickers which is what is analyzed in Section 6.5.1.

set.seed(0612)         
mu <- mean( Snickers )
sigma <- sd( Snickers )
bigsnickers <- rnorm( 100000, mean = mu, sd = sigma )

The set.seed function is used here to ensure that the dataset we generate is the same each time we run the code. We set the mu and sigma to be equal to the mean and (sample) standard deviation of the Snickers dataset. We used the rnorm function to generate one hundred thousand random variables that follow the Normal distribution with these values as we will define in Chapter 7.

Remark. While the use of set.seed may seem to remove the randomness of it, the process of writing a book requires us to run the code of R chunks many times and we need to be able to know what values we will encounter so that words used in the book match the actual data generated. This is due to the desire to publish our results and does not invalidate the “randomness” of the dataset. We encourage the reader to run the code above without the set.seed line or with a different value within the set.seed function and compare their dataset with the one analyzed in Section 6.5.1.

See the website for the San Diego Zoo Safari Park.↩︎
Further information can be found on Wikipedia.↩︎
Further information can be found on Wikipedia.↩︎
Journal of Statistics Education Volume 14, Number 3 (2006), Link.↩︎
We will see that this is a very valid assumption using the Law of Large Numbers which is Theorem 6.1.↩︎
The concept of a generic discrete set is a bit tricky to define, but the curious reader may refer to Wikipedia for more information.↩︎
This is exactly what the Law of Large Numbers, Theorem 6.1 will tell us in Section 6.3.↩︎
We actually only have 5997 observations. The process of “cleaning up” the data to get to the Pigs dataframe can be found in the appendix Section 6.7.1.↩︎
The Law of Large Numbers can often be misunderstood. If, for example, you flip a quarter 9 times and observe 9 Heads, the Law of Large Numbers does not somehow “change” the probability that the next flip should be a Tails. For every trial, a fair coin has $P(\text{Tails}) = \frac{1}{2}$ regardless of what has happened prior to the flip. However, what the Law of Large Numbers does say is that the chance of the coin not being close to 50% heads after a lot of flips is small and the chance gets smaller and smaller as the number of flips increases.↩︎
We will not define what a True Probability is in this book as it is a very hard and debated topic. The curious reader is welcome to head down a rabbit hole by starting Here on Wikipedia.↩︎
C Purtill, “A Statistician Got Curious about M&M Colors and Went on an Endearingly Geeky Quest for Answers,” Quartz, March 15, 2017, https://qz.com/918008/the-color-distribution-of-mms-as-determined-by-a-phd-in-statistics/.↩︎
This serves as an acknowledgement that the ten thousand values used were generated by R using random numbers. A discussion of this set of simulated data can be found in Section 6.7.2.2.↩︎
We will use the term curve to be the graph of a function even if the graph does not actually “curve” in the more basic sense.↩︎
The advanced reader may notice the concept of an integral in this function and the ones that follow. This is indeed the case, but this book is designed to be taught to students who have not (necessarily) taken any calculus.↩︎
The main reason for not providing graphs of distribution or quantile functions is that Statypus is written as a text for a non-Calculus based introductory statistics course. The curious reader can see Wikipedia to learn more about these functions.↩︎
“Mind your Ps and Qs” is an English language expression meaning “mind your manners”, “mind your language”, “be on your best behaviour”, or “watch what you’re doing”. See Wikipedia for information about the possible origins of the expression.↩︎
We will not go into much detail about factor here, but you can find more about it using ?factor.↩︎
We acknowledge the seeming contradiction of being pedantic about mass versus weight and then making the conversion ourselves. However, we will be restricting our view to Snickers bars as they exist on the surface of the Earth so that the change is essentially a unit conversion.↩︎
This serves as a reminder that R handles things in a case sensitive way. R views snickers as a totally different vector than Snickers. We do remind the reader that if you type in the string sni into an R script or the RStudio console, it will populate all data and functions that begin with the string sni with any combination of upper and lower case letters. This is why we encourage readers to use the auto-complete feature to ensure that they are choosing the correct spelling of items, including the case of the letters. The author fully admits that they almost always type view when he wants the function View and then relies on the auto complete to make the change. At this point, the author should know it is an upper case V, but muscle memory is sometimes hard to rebuild.↩︎